Selamat datang, Kali ini kita akan berbagi tentang Aplikasi Penerapan Persamaan Kuadrat dalam Kehidupan. Silahkan dibaca baik-baik tentang Aplikasi Penerapan Persamaan Kuadrat dalam Kehidupan ini ya.
Gerak suatu objek yang dilempar ke atas merupakan salah satu penerapan dari persamaan kuadrat dalam kehidupan sehari-hari. Gerak objek tersebut dapat dirumuskan dengan rumus h = –5t2 + vt + k, dengan h adalah ketinggian objek tersebut dalam meter, t adalah waktu dalam detik, dan v adalah kecepatan awal dalam meter per sekon. Konstanta kmerepresentasikan ketinggian awal dari objek dari permukaan tanah. Untuk lebih memahami mengenai gerak objek yang dilempar ke atas, perhatikan contoh berikut.
Contoh 1: Menyelesaikan Penerapan Persamaan Kuadrat
Seorang anak berdiri di atas tebing yang memiliki ketinggian 5 m dari permukaan tanah, melempar bola ke atas dengan kecepatan awal 20 m/s (anggap bola dilepaskan ketika berada 1 m di atas permukaan tebing di mana anak tersebut berdiri). Tentukan (a) tinggi bola setelah 3 detik, dan (b) waktu yang dibutuhkan agar bola tersebut sampai di permukaan tanah.

Pembahasan Dengan menggunakan informasi yang diberikan soal, kita memperoleh h = –5t2 + 20t + 6. Untuk menentukan tinggi bola setelah 3 detik, substitusikan t = 3 ke dalam persamaan tersebut.

Apabila bola sampai di permukaan tanah, maka ketinggian bola tersebut adalah 0 meter. Sehingga dengan mensubstitusi h = 0 diperoleh,

Karena waktu tidak pernah negatif, maka waktu yang diperlukan agar bola tersebut sampai di permukaan tanah adalah 4,28 detik.
Contoh 2: Permasalahan Pelanggan Telepon Genggam
Dari tahun 1995 sampai 2002, banyaknya pelanggan telepon genggam N (dalam juta orang) dapat dimodelkan oleh persamaan N = 17,4x2 + 36,1x + 83,3, dengan x = 0 merepresentasikan tahun 1995 [Sumber: Data dari 2005 Statistical Abstract of the United States, Tabel 1.372, hal. 870]. Pada tahun berapa banyaknya pelanggan telepon genggam mencapai angka 3.750 juta?
Pembahasan Dari soal diketahui bahwa N = 17,4x2 + 36,1x + 83,3 dan kita diminta untuk menentukan tahun ketika banyaknya pelanggan telepon genggam mencapai 3.750 juta. Dengan kata lain, kita diminta untuk menentukan nilai 1995 + x ketika N = 3.750.
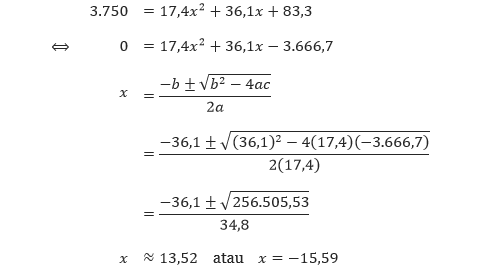
Karena waktu tidak pernah negatif, maka kita simpulkan bahwa 13,52 tahun setelah tahun 1995, yaitu tahun 2008, banyaknya pelanggan telepon genggam mencapai angka 3.750 juta
No comments:
Post a Comment