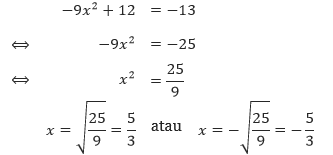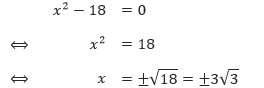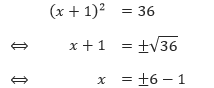Diskriminan Persamaan Kuadrat

Perhatikan bahwa √X merupakan bilangan real jika dan hanya jika X ≥ 0. Karena selesaian persamaan kuadrat memuat bentuk akar √(b2 – 4ac), bentuk aljabar b2 – 4ac, yang disebut diskriminan, akan menentukan sifat dan banyaknya selesaian/akar dari persamaan kuadrat yang diberikan.

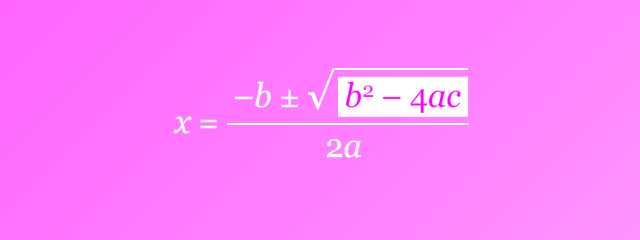
Diskriminan dari Persamaan Kuadrat

Untuk ax2 + bx + c = 0, dengan a ≠ 0,

1. Jika b2 – 4ac = 0, maka persamaan kuadrat tersebut memiliki satu selesaian bilangan real.
2. Jika b2 – 4ac > 0, maka persamaan kuadrat tersebut memiliki dua selesaian bilangan real.
3. Jika b2 – 4ac < 0, maka persamaan kuadrat tersebut memiliki dua selesaian bilangan kompleks.

Catatan Bilangan kompleks adalah bilangan yang dapat dinyatakan ke dalam a + bi, dengan a dan b bilangan real, dan i = √(–1). Misalnya, 1 + √(–8) adalah bilangan kompleks karena 1 + √8 ∙ √–1 = 1 + 2√2 i. Karena semua bilangan real dapat dinyatakan ke dalam bentuk a + bi (dengan b = 0), maka himpunan bilangan real merupakan himpunan bagian dari himpunan bilangan kompleks.

Dengan menganalisis secara lebih jauh mengenai diskriminan akan diperoleh beberapa sifat dari persamaan kuadrat tertentu. Jika a, b, dan c adalah bilangan-bilangan rasional dan diskriminannya merupakan bilangan kuadrat tidak nol, maka akan ada dua akar rasional dari persamaan tersebut. Atau dengan kata lain, persamaan kuadrat tersebut dapat diselesaikan dengan menggunakan pemfaktoran. Jika diskriminannya bukan bilangan kuadrat, maka akan ada dua akar yang sekawan. Dan jika diskriminannya nol, maka akan ada satu akar yang merupakan bilangan rasional, dan persamaan kuadratnya merupakan kuadrat dari binomial.

Contoh: Menggunakan Diskriminan untuk Analisis Selesaian

Gunakan diskriminan untuk menganalisis persamaan-persamaan kuadrat berikut apakah memiliki akar bilangan real. Jika iya, nyatakan apakah akar-akar tersebut merupakan bilangan rasional atau irasional, dan apakah persamaan kuadrat tersebut dapat difaktorkan atau tidak.

1. 2x2 + 5x + 2 = 0
2. x2 – 4x + 7 = 0
3. 4x2 – 20x + 25 = 0

Pembahasan

1. Persamaan 2x2 + 5x + 2 = 0 memiliki a = 2, b = 5, dan c = 2. Sehingga,
   
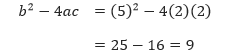
   Kita peroleh bahwa diskriminan dari persamaan kuadrat tersebut merupakan bilangan kuadrat tidak nol. Maka persamaan tersebut memiliki 2 akar rasional dan dapat difaktorkan.
2. Dari persamaan x2 – 4x + 7 = 0 kita peroleh a = 1, b = –4, dan c = 7.
   
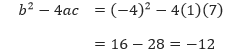
   Karena –12 < 0, maka persamaan kuadrat tersebut memiliki dua akar bilangan kompleks dan tidak dapat difaktorkan.
3. Persamaan kuadrat 4x2 – 20x + 25 = 0 memiliki a = 4, b = –20, dan c = 25. Maka,
   
   Karena diskriminannya nol, maka persamaan kuadrat tersebut memiliki satu akar bilangan rasional dan dapat difaktorkan.

Perhatikan kembali contoh (2) di atas. Diskriminan persamaan kuadrat pada contoh soal tersebut adalah –12, yang berarti bahwa persamaan tersebut memiliki dua selesaian bilangan kompleks, yaitu

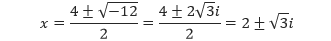
Akar-akar tersebut dapat dituliskan sebagai x = 2 + √3 i dan x = 2 – √3 i, yang merupakan dua bilangan kompleks yang sekawan

Contoh Barisan Rekursif

Rekursi adalah salah satu ide penting dalam ilmu komputer. Untuk menyelesaikan suatu masalah secara rekursif, kita harus memecah masalah tersebut menjadi beberapa submasalah yang masing-masing memiliki bentuk yang sama dengan masalah awal. Untuk melakukan hal ini, kita harus menemukan suatu cara sedemikian sehingga ketika proses diulang beberapa kali, submasalah terakhir menjadi mudah diselesaikan dan solusi dari submasalah-submasalah yang terbentuk dapat dihimpun bersama untuk membentuk solusi dari masalah aslinya.

Mungkin bagian tersulit dalam memecahkan masalah secara rekursif adalah ketika pada tahap menentukan bagaimana mengetahui solusi dari submasalah-submasalah tersebut akan memberikan solusi pada masalah asli secara keseluruhan. Andaikan kita tahu solusi dari submasalahnya, bagaimana kita menggunakan solusi tersebut untuk menyelesaikan permasalahan yang lebih luas merupakan hal yang tidak mudah. Anggapan bahwa submasalah yang sudah terselesaikan ini biasa disebut sebagai anggapan perulangan rekursif. Anggapan perulangan rekursif ini serupa dengan hipotesis induksi pada pembuktian dengan induksi matematika.

Contoh 1: Menara Hanoi

Pada tahun 1883 seorang matematikawan berkebangsaan Prancis, Édouard Lucas, menemukan suatu permainan yang disebut Menara Hanoi (La Tour D’Hanoï). Permainan ini memiliki 8 cakram kayu dengan lubang di tengahnya, yang disusun dari ukuran terkecil ke terbesar pada salah satu tiang dari total 3 tiang yang ada. Jiplakan sampul dari kotak Menara Hanoi waktu itu dapat dilihat pada gambar berikut.

Pemain dari permainan ini diminta untuk memindahkan semua cakram dari tiang satu ke tiang lainnya, dengan tidak menempatkan cakram yang lebih besar di atas cakram yang lebih kecil. Aturan dari permainan ini didasarkan pada legenda di India:

Pada tangga dari altar kuil di Benares, selama bertahun-tahun lamanya, Brahmana telah memindahkan menara 64 cakram emas dari satu tiang ke tiang lainnya; satu demi satu, dan tidak pernah sama sekali menempatkan cakram yang lebih besar di atas cakram yang lebih kecil. Ketika semua cakram tersebut sudah dipindahkan, maka Brahmana akan jatuh, dan itu merupakan akhir dari dunia.

Pada waktu itu, permainan ini menawarkan hadiah sebesar 10 ribu franc (atau sekitar 13 juta rupiah) kepada siapa saja yang dapat memindahkan 64 cakram dengan menggunakan tangan dan dengan mengikuti aturan permainan ini. Andaikan kamu memindahkan cakram-cakram tersebut dengan langkah-langkah yang seefisien mungkin, berapa langkah yang kamu butuhkan untuk memenangkan hadiah tersebut?

Pembahasan Untuk menyelesaikan permasalahan menara Hanoi di atas, sebaiknya kita perumum permasalahannya untuk n adalah banyaknya cakram yang akan dipindahkan. Untuk memindahkan semua cakram dari satu tiang ke tiang lainnya, perhatikan ilustrasi berikut.

Pada gambar (i), terdapat n cakram yang harus dipindahkan ke tiang yang lainnya. Misalkan, banyaknya langkah yang harus dilakukan untuk memindahkan n cakram tersebut kita simbolkan dengan mn. Pertama, kita harus memindahkan sejumlah n – 1 cakram teratas ke tiang lainnya, misalkan tiang C. Sehingga, banyaknya langkah yang harus kita lakukan adalah mn – 1 (gambar (ii)). Selanjutnya, kita pindah satu cakram yang tersisa ke tiang B (tiang yang masih kosong). Untuk memindahkan satu cakram tersebut, kita melakukan 1 langkah. Dan terakhir, kita pindahkan sejumlah n – 1 cakram pada tiang C ke tiang B. Proses ini membutuhkan mn – 1 langkah. Sehingga, banyaknya langkah yang diperlukan untuk memindahkan n cakram dapat dirumuskan sebagai berikut.

Untuk menentukan kondisi awalnya, kita perhatikan kembali definisi dari barisan tersebut. Karena hanya 1 langkah yang diperlukan untuk memindahkan 1 cakram dari satu tiang ke tiang lainnya, maka

Sehingga, barisan m1, m2, m3, …, dapat didefinisikan secara rekursif sebagai berikut: Untuk semua bilangan bulat n ≥ 2

Berikut ini perhitungan dari 5 suku selanjutnya.

Kembali kepada legenda India, misalkan kita memindahkan cakram-cakram tersebut dengan kecapatan 1 langkah setiap detik. Maka waktu yang diperlukan dari awal penciptaan sampai akhir dunia adalah m64 detik. Untuk menentukan m64, kita dapat menggunakan kalkulator untuk melanjutkan proses di atas. Nilai dari m64 adalah sekitar,

Dan tahukah kamu, nilai di atas, 584,5 miliar tahun, mendekati usia semesta kita yang yang diperoleh dengan menggunakan kajian ilmiah!

Distribusi Binomial

Percobaan binomial merupakan suatu percobaan yang memenuhi empat syarat berikut:

1. Terdapat n kali percobaan.
2. Masing-masing percobaan hanya dapat menghasilkan dua kemungkinan, atau hasil yang diperoleh dapat disederhanakan menjadi dua kemungkinan. Hasil yang diperoleh tersebut dapat dianggap sebagai hasil yang sukses atau gagal.
3. Hasil dari masing-masing percobaan haruslah saling bebas.
4. Peluang untuk sukses harus sama untuk setiap percobaan.

---

Suatu percobaan binomial dan hasilnya memberikan distribusi peluang khusus yang disebut sebagai distribusi binomial.

Hasil-hasil percobaan binomial dan peluang yang bersesuaian dari hasil tersebut dinamakan distribusi binomial.

Dalam percobaan binomial, hasil-hasilnya seringkali diklasifikasikan sebagai hasil yang sukses atau gagal. Sebagai contoh, jawaban benar suatu pertanyaan pilihan ganda dapat diklasifikasikan sebagai hasil yang sukses, sehingga pilihan jawaban lainnya merupakan jawaban yang salah dan diklasifikasikan sebagai hasil yang gagal. Notasi-notasi yang umumnya digunakan dalam percobaan binomial dan distribusi binomial adalah sebagai berikut.

Notasi	Keterangan
P(S)	Simbol untuk peluang sukses.
P(F)	Simbol untuk peluang gagal.
p	Peluang sukes.
q	Peluang gagal.
	P(S) = p dan P(F) = 1 – p = q
n	Banyaknya percobaan
X	Banyaknya sukses dalam n kali percobaan
Perhatikan bahwa 0 ≤ X ≤ n dan X = 0, 1, 2, 3, …, n.

Peluang sukses dalam percobaan binomial dapat dihitung dengan menggunakan rumus berikut.

---

Rumus Peluang Binomial

Dalam suatu percobaan binomial, peluang untuk mendapatkan tepat X sukses dalam npercobaan adalah

---

Untuk mengetahui bagaimana ilustrasi dari rumus peluang binomial tersebut bermula, perhatikan Contoh 1 berikut.

Contoh 1: Melempar Koin

Suatu koin dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka.

Pembahasan Permasalahan ini dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari pelemparan satu koin sebanyak tiga kali adalah

S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}

Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua angka adalah 3/8 atau 0,375.

Dengan melihat kembali Contoh 1 dari sudut pandang percobaan binomial, maka contoh tersebut memenuhi keempat kriteria percobaan binomial.

1. Terdapat tiga kali percobaan.
2. Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
3. Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
4. Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.

Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-nilai tersebut ke dalam rumus, kita mendapatkan

Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang sampel.

Contoh 1 tersebut juga dapat digunakan untuk menjelaskan rumus peluang binomial. Pertama, perhatikan bahwa terdapat tiga cara untuk mendapatkan tepat dua angka dan satu gambar dari delapan kemungkinan. Ketiga cara tersebut adalah AAG, AGA, dan GAA. Sehingga, dalam kasus ini banyaknya cara kita mendapatkan dua angka dari pelemparan koin sebanyak tiga kali adalah 3C2, atau 3. Secara umum, banyak cara untuk mendapatkanX sukses dari n percobaan tanpa memperhitungkan urutannya adalah

Ini merupakan bagian pertama rumus binomial. (Beberapa kalkulator dapat digunakan untuk menghitung kombinasi tersebut).

Selanjutnya, masing-masing sukses memiliki peluang ½ dan muncul sebanyak dua kali. Demikian juga masing-masing gagal memiliki peluang ½ dan muncul sekali. Sehingga akan memberikan,

pada rumus binomial. Sehingga apabila masing-masing percobaan sukses sukses memiliki peluang p dan muncul X kali serta peluang gagalnya adalah q dan muncul n – X kali, maka dengan menuliskan peluang percobaan sukses kita akan mendapatkan rumus binomial.

Soal dan Pembahasan Program Linear

Seorang pedagang sepeda ingin membeli 25 sepeda untuk persediaan. Ia ingin membeli sepeda gunung dengan harga Rp 1.500.000,00 per buah dan sepeda balap dengan harga Rp 2.000.000,00 per buah. Ia berencana tidak akan mengeluarkan uang lebih dari Rp 42.000.000,00. Jika keuntungan sebuah sepeda gunung Rp 500.000,00 dan sebuah sepeda balap Rp 600.000,00, maka keuntungan maksimum yang diterima pedagang adalah …

Pembahasan Tanpa membuat tabel, kita dapat memodelkan kendala-kendala dari permasalahan tersebut sebagai berikut.

x + y ≤ 25,
1.500.000x + 2.000.000y ≤ 42.000.000,
x ≥ 0, y ≥ 0,
x dan y bilangan cacah.

Dengan fungsi objektifnya adalah f(x, y) = 500.000x + 600.000y. Sehingga apabila digambarkan, daerah selesaiannya akan nampak seperti berikut.

Selanjutnya kita tentukan titik potong grafik persamaan 1.500.000x + 2.000.000y = 42.000.000 dan x + y = 25.

Sehingga,

Diperoleh,

Selanjutnya kita lakukan uji titik pojok ke dalam fungsi objektifnya.

Jadi, keuntungan maksimum yang diterima pedagang adalah Rp 13.400.000,00.

Untuk mendownload 10 soal beserta pembahasan selengkapnya, silahkan klik di sini. 

Penyelesaian Persamaan Kuadrat dengan Sifat Akar Persamaan

Persamaan x2 = 25 dapat diselesaikan dengan menggunakan pemfaktoran. Bentuk standar dari x2 = 25 adalah x2 – 25 = 0 yang dapat difaktorkan menjadi (x – 5)(x + 5) = 0. Sehingga, solusi-solusi dari persamaan kuadrat tersebut adalah x = 5 atau x = –5, yang merupakan bilangan positif dan negatif dari akar kuadrat 25. Hasil ini memberikan suatu metode untuk menyelesaikan suatu persamaan kuadrat yang berbentuk X2 = k, yang selanjutnya disebut sifat akar kuadrat dari suatu persamaan.

Sifat Akar Kuadrat dari Suatu Persamaan
Jika X merepresentasikan suatu bentuk aljabar dan X2 = k, maka X = √k atau X = –√k, atau juga dapat dituliskan X = ±√k

Untuk lebih memahami penggunaan metode ini dalam menyelesaikan persamaan kuadrat, perhatikan contoh soal berikut.

Contoh 3: Penggunaan Sifat Akar Kuadrat dari Suatu Persamaan

Gunakan sifat akar kuadrat dari suatu persamaan untuk menyelesaikan masing-masing persamaan berikut.

1. –9x2 + 12 = –13
2. x2 – 18 = 0
3. (x + 1)2 = 36

Pembahasan

1. Persamaan –9x2 + 12 = –13 tidak berbentuk X2 = k. Sehingga kita harus mengubah persamaan kuadrat tersebut menjadi bentuk seperti itu.
   
   Sehingga, selesaian dari persamaan –9x2 + 12 = –13 adalah x = 5/3 atau x = –5/3.
2. Bentuk X2 = k dari x2 – 18 = 0 adalah x2 = 18. Sehingga,
   
   Jadi, selesaian dari persamaan x2 – 18 = 0 adalah x = 3√3 atau x = –3√3.
3. Persamaan (x + 1)2 = 36 sudah memiliki bentuk X2 = k. Sehingga,
   
   Sehingga, selesaian dari persamaan (x + 1)2 = 36 adalah x = 6 – 1 = 5 atau x = –6 – 1 = –7.

Untuk persamaan yang berbentuk (ax + b)2 = k (seperti contoh 3), dapat juga diselesaikan dengan menggunakan pemfaktoran. Akan tetapi kita harus menulis pangkat dua binomial tersebut ke dalam ekspansi/bentuk panjangnya, kemudian menyederhanakan persamaan yang diperoleh agar ruas kanan sama dengan nol dan terakhir, kita dapat memfaktorkan persamaan tersebut untuk menentukan selesaian-selesaiannya. Dengan menggunakan sifat akar kuadrat dari suatu persamaan, kita dapat menyelesaikan persamaan yang berbentuk (ax + b)2 = k secara lebih mudah.

Penyelesaian Persamaan Kuadrat dengan Kuadrat Sempurna

Perhatikan persamaan kuadrat, (x – 5)2 = 24. Jika kita menuliskan kuadrat dari binomial tersebut menjadi bentuk panjangnya, kita memperoleh x2 – 10x + 25 = 24. Sehingga, apabila persamaan tersebut dituliskan dalam bentuk standar maka akan menjadi x2 – 10x+ 1 = 0, yang sangat sulit dipecah ke dalam perkalian faktor-faktornya karena faktor-faktor persamaan tersebut merupakan bilangan irasional. Dengan membalik proses di atas, kita akan mendapatkan strategi untuk menyelesaikan persamaan kuadrat yang tidak dapat diselesaikan dengan pemfaktoran. Strategi tersebut selanjutnya disebut caramelengkapkan kuadrat. Perhatikan ilustrasi berikut.

Pada umumnya, setelah memindah konstanta ke ruas yang lain (lihat baris kedua), bilangan yang dapat “melengkapi kuadrat” dapat ditentukan dengan mengkuadratkan setengah dari koefisien suku linear: [1/2 ∙ (10)]2 = 25. Untuk lebih jelasnya, perhatikan contoh berikut.

Contoh 1: Menyelesaikan Persamaan Kuadrat dengan Melengkapkan Kuadrat

Dengan menggunakan cara melengkapkan kuadrat, selesaikanlah x2 + 13 = 6x.

Pembahasan Karena x2 + 13 = 6x tidak dalam bentuk standar, maka kita harus menuliskannya ke dalam bentuk standar terlebih dahulu.

Proses melengkapkan kuadrat dapat dilakukan terhadap semua persamaan kuadrat dengan koefisien suku-x2, a = 1. Jika koefisien dari suku-x2 tidak 1, maka kita harus membagi persamaan tersebut dengan a. Berikut ini langkah-langkah dalam menyelesaikan persamaan kuadrat dengan cara melengkapkan kuadrat.

Melengkapkan Kuadrat dengan Cara Melengkapkan Kuadrat

Untuk menyelesaikan ax2 + bx + c = 0 dengan cara melengkapkan kuadrat:

1. Pindahkan konstanta c ke ruas kanan.
2. Bagi kedua ruas dengan koefisien suku-x2, a.
3. Hitung [1/2 ∙ (b/a)]2 dan jumlahkan kedua ruas dengan hasilnya.
4. Faktorkan ruas kanan sebagai kuadrat binomial; sederhanakan ruas kanan.
5. Selesaikan dengan menggunakan sifat akar kuadrat dari suatu persamaan.

Contoh 2: Menyelesaikan Persamaan Kuadrat dengan Melengkapkan Kuadrat

Dengan melengkapkan kuadrat, selesaikan –3x2 + 1 = 4x.

Pembahasan Bentuk standar dari –3x2 + 1 = 4x adalah –3x2 – 4x + 1 = 0. Sehingga,

Jadi, selesaian-selesaian dari persamaan –3x2 + 1 = 4x  adalah x = –2/3 + √7/3 atau x = –2/3 – √7/3