Selamat datang, Kali ini kita akan berbagi tentang Contoh Soal dan Pembahasan Menggambar Fungsi Kuadrat. Silahkan dibaca baik-baik tentang Contoh Soal dan Pembahasan Menggambar Fungsi Kuadrat ini ya.
BAGIAN I
Fungsi kuadrat merupakan suatu fungsi yang memiliki satu variabel yang pangkat tertingginya adalah 2. Fungsi kuadrat memiliki bentuk umum f(x) = ax2 + bx + c, dengana, b, c bilangan real dan a ≠ 0. Pada pembahasan ini akan ditunjukkan bagaimana cara melukis grafik fungsi kuadrat, khususnya grafik fungsi f(x) = x2 dan f(x) = –x2. Mengapa memilih fungsi-fungsi kuadrat tersebut? Karena fungsi-fungsi tersebut merupakan fungsi-fungsi kuadrat yang paling sederhana.
Melukis Grafik Fungsi f(x) = x2
Sebelum melukis grafik fungsi f(x) = x2, perlu diketahui bahwa semua fungsi kuadrat merupakan fungsi kontinu. Sehingga apabila dilukiskan grafik fungsinya, akan terbentuk grafik fungsi yang halus. Selain itu, fungsi f(x) = x2 merupakan fungsi genap, yaitu fungsi yang nilai f(x) = f(–x). Grafik dari fungsi genap memiliki sumbu simetri pada sumbu-y. Berikut ini langkah-langkah dalam melukis grafik fungsi f(x) = x2.
- Cacahlah titik-titik yang dilalui oleh grafik fungsi f(x) = x2. Karena grafik fungsi tersebut memiliki sumbu simetri pada sumbu-y, pilihlah x = – 3, – 2, – 1, 0, 1, 2, 3.

- Lukislah titik-titik dengan koordinat (x, f(x)) pada koordinat Cartesius.

- Hubungkan titik-titik tersebut dengan menggunakan kurva halus. Grafik yang terbentuk merupakan grafik fungsi f(x) = x2.

Selanjutnya akan dilukis grafik dari fungsi f(x) = –x2. Dengan langkah-langkah yang sama dengan melukis grafik fungsi f(x) = x2 di atas, melukis grafik fungsi f(x) = –x2 dapat ditunjukkan oleh ilustrasi berikut.

BAGIAN 2
Bagaimana dengan grafik-grafik fungsi kuadrat lainnya? Seperti diketahui, bentuk umum dari fungsi kuadrat adalah f(x) = ax2 +bx + c. Pada pembahasan ini akan ditunjukkan cara melukis grafik fungsi kuadrat yang memiliki nilai a = 1 (f(x) = x2 + bx + c). Dalam melukis grafik fungsi kuadrat dengan a = 1 dapat digunakan proses transformasi grafik fungsi f(x) = x2. Berikut ini beberapa jenis grafik fungsi kuadrat yang merupakan hasil transformasi dari grafik fungsi f(x) = x2.
Grafik Fungsi f(x) = (x – p)2
Grafik fungsi f(x) = (x – p)2, p bilangan real positif, merupakan hasil pergeseran/translasi grafik f(x) = x2 ke kanan sejauh a. Apabila fungsi f(x) = x2 memiliki sumbu simetri pada sumbu-y, maka fungsi f(x) = (x – a)2 memiliki sumbu simetri pada garis x = a. Misalkan untuk fungsi f(x) = (x – 2)2 = x2 – 4x + 4. Grafik ini merupakan hasil translasi grafik f(x) =x2 ke kanan sejauh 2 satuan sehingga sumbu simetrinya adalah x = 2. Perhatikan gambar berikut:

Sedangkan grafik fungsi f(x) = (x + p)2 merupakan hasil pergeseran grafik fungsi f(x) = x2ke kiri sejauh p satuan.
Grafik Fungsi f(x) = x2 + q
Grafik fungsi f(x) = x2 + q, q bilangan real positif, merupakan hasil translasi grafik f(x) = x2ke atas sejauh q satuan. Misalkan f(x) = x2 + 3. Grafik dari fungsi tersebut merupakan hasil translasi dari grafik f(x) = x2 ke atas sejauh 3 satuan. Perhatikan gambar berikut.

Sedangkan grafik fungsi f(x) = x2 – q merupakan hasil translasi grafik f(x) = x2 ke bawahsejauh q satuan.
Tips dan Trik Menggambar Grafik Fungsi Kuadrat
Dalam melukis grafik fungsi kuadrat yang berbentuk f(x) = x2 + bx + c, sebaiknya diubah dulu fungsi tersebut menjadi bentuk f(x) = (x – p)2 + q. Misalkan: lukis grafik fungsi f(x) =x2 + 6x + 7. Fungsi kuadrat tersebut ekuivalen dengan fungsi f(x) = (x + 3)2 – 2. Sehingga grafiknya merupakan hasil translasi grafik f(x) = x2 ke kiri sejauh 3 satuan, kemudian dilanjutkan ke bawah sejauh 2 satuan. Ilustrasi dari melukis grafik fungsi tersebut dapat ditunjukkan sebagai berikut.

BAGIAN 3
pembahasan ini akan ditunjukkan bagaimana melukis grafik fungsi kuadrat yang berbentuk
f(x) = ax2 + bx + c, dengan a bilangan real bukan nol (a ≠ 0) dan bukan satu (a ≠ 1).
f(x) = ax2 + bx + c, dengan a bilangan real bukan nol (a ≠ 0) dan bukan satu (a ≠ 1).
Sebelum membahas bagaimana melukis grafik fungsi kuadrat yang dimaksud, akan dibahas mengenai topik melengkapkan kuadrat. Bentuk fungsi kuadrat f(x) = ax2 + bx+ c dapat diubah bentuknya menjadi bentuk lain, dengan teknik melengkapkan kuadrat. Perhatikan gambar di bawah ini.
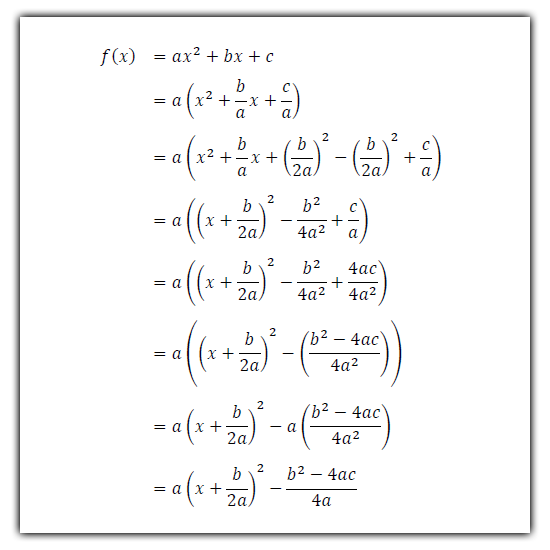
Dari fungsi di atas dapat diketahui dengan mudah bahwa fungsi tersebut memiliki titik ekstrim, (xp, yp). Titik ekstrim dapat berupa nilai maksimum ataupun maksimum suatu fungsi kuadrat tersebut, tergantung nilai a. Apabila a positif maka titik tersebut adalah nilai minimum, apabila a negatif maka titik tersebut merupakan nilai maksimum. Titik ekstrim dapat ditentukan apabila yang dikuadratkan pada fungsi kuadrat di atas (setelah diubah dengan melengkapkan kuadrat) adalah nol. Mengapa? Karena bentuk kuadrat memiliki nilai minimum nol.

Grafik Fungsi Kuadrat f(x) = ax2 + bx + c.
Untuk melukis grafik fungsi kuadrat f(x) = ax2 + bx + c, terlebih dahulu cari titik ekstrimnya kemudian cari 2 titik lainnya yang letaknya di kanan dan kiri titik ekstrim tersebut. Setelah itu, plot ketiga titik tersebut pada koordinat Cartesius dan hubungkan dengan kurva halus. Misalkan akan dilukis grafik fungsi f(x) = 2x2 –12x + 17. Grafik fungsi tersebut memiliki nilai a = 2, b = – 12, dan c = 17. Sehingga titik ekstrimnya adalah (3, –1). Dengan substitusi x = 0 dan x = 6 ke fungsi kuadrat tersebut diperoleh 2 titik lainnya adalah (0, 17) dan (6, 17). Berikut adalah grafik dari fungsi f(x) = 2x2 –12x + 17.

No comments:
Post a Comment