Selamat datang, Kali ini kita akan berbagi tentang Menyusun Fungsi Kuadrat. Silahkan dibaca baik-baik tentang Menyusun Fungsi Kuadrat ini ya.
Fungsi kuadrat (quadratic function) adalah fungsi polinomial yang berderajat dua. Bentuk umum dari fungsi kuadrat adalah f(x) = ax2 + bx + c, a ≠ 0. Fungsi kuadrat dapat memotong sumbu-x 2 kali, 1 kali, atau tidak memotong sumbu-x sama sekali.

Pada artikel ini akan dibahas fungsi kuadrat yang memotong sumbu-x minimal di satu titik, misalkan di titik-titik (x1, 0) dan (x2, 0). Sehingga didapatkan f(x1) = f(x2) = 0. Apabila fungsi kuadrat yang memotong sumbu-x di dua titik tersebut melalui titik (x3, y3), maka fungsi kuadrat tersebut dapat ditentukan bentuknya, yaitu sebagai berikut:

Contoh Soal
Susunlah fungsi kuadrat yang memotong sumbu-x di titik (2, 0) dan titik (–1, 0) serta melalui titik (3, 12)!
Jawab:
Karena fungsi kuadrat yang dimaksud melalui titik (3, 12) serta memotong sumbu-x di titik (2, 0) dan titik (–1, 0), maka kita cukup mensubstitusikan 3 pada x, 12 pada f(x), serta absis-absis titik potong sumbu-x pada x1 dan x2. Sehingga,
Karena fungsi kuadrat yang dimaksud melalui titik (3, 12) serta memotong sumbu-x di titik (2, 0) dan titik (–1, 0), maka kita cukup mensubstitusikan 3 pada x, 12 pada f(x), serta absis-absis titik potong sumbu-x pada x1 dan x2. Sehingga,

Setelah diperoleh a = 3, substitusikan a tersebut pada rumus dengan membiarkan x danf(x).

Sehingga diperoleh fungsi kuadrat yang dimaksud adalah f(x) = 3x2 – 3x – 6. Untuk mengecek hasil yang diperoleh, mari kita uji fungsi tersebut apakah melalui titi-titik (2, 0), (–1, 0), dan (3, 12).
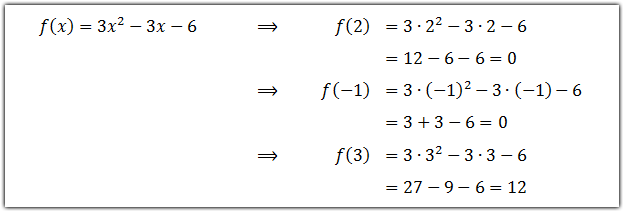
Sehingga fungsi kuadrat yang diperoleh memenuhi permintaan soal. Untuk menguji kompetensi mengenai materi ini silahkan kerjakan soal berikut.
Perhatikan gambar di bawah!

Tentukanlah fungsi kuadrat yang grafiknya digambarkan seperti gambar di atas!
Fungsi kuadrat memiliki grafik yang berbentuk parabola yang terbuka ke atas atau ke bawah. Sehingga fungsi kuadrat dapat memiliki nilai minimum ataupun maksimum, tergantung dari koefisien x2 (a) fungsi kuadrat tersebut. Apabila nilai a positif, maka fungsi kuadrat tersebut memiliki nilai minimum. Sedangkan apabila nilai a negatif, fungsi kuadrat tersebut memiliki nilai maksimum. Titik di mana nilai maksimum/minimum dari fungsi kuadrat tersebut disebut titik ekstrim, disimbolkan (xp, yp).
Fungsi kuadrat yang memiliki titik ekstrim (xp, yp) dan melalui satu titik lain dapat disusun dengan menggunakan rumus berikut:
y = a(x – xp) + yp
Untuk lebih memahami mengenai topik menyusun fungsi kuadrat apabila diketahui titik ekstrim dan satu titik lain yang dilaluinya, perhatikan contoh soal berikut.
Contoh Soal
Susunlah fungsi kuadrat yang memiliki titik ekstrim di (2, –5) dan melalui titik (1, 4)!
Pembahasan
Fungsi kuadrat yang memiliki titik ekstrim di (2, –5) dan melalui titik (1, 4) dapat ditentukan sebagai berikut:
Fungsi kuadrat yang memiliki titik ekstrim di (2, –5) dan melalui titik (1, 4) dapat ditentukan sebagai berikut:

Untuk a = 9, diperoleh

Jadi, fungsi kuadrat yang memiliki titik ekstrim (2, –5) dan melalui titik (1, 4) adalah y = 9x2 – 36x + 31.
Yang akan dibicarakan di sini adalah menyusun fungsi kuadrat jika diketahui ketiga titik yang dilaluinya, titik ekstrim tidak masuk dalam ketiga titik tersebut.
Untuk menyusun fungsi kuadrat jika diketahui ketiga titik yang dilaluinya digunakan bentuk umum dari fungsi kuadrat berikut:

Dengan a, b, dan c bilangan real, serta a ≠ 0.
Untuk mengetahui bagaimana menyusun fungsi kuadrat jika diketahui ketiga titik yang dilaluinya, perhatikan contoh soal berikut.
Contoh Soal
Tentukan fungsi kuadrat yang melalui titik-titik (–1, 6) dan (2, 12) serta memotong sumbu-y pada y = 2!
Jawab
Fungsi kuadrat yang akan dicari memotong sumbu-y pada y = 2, atau dengan kata lain memotong sumbu-y di titik (0, 2). Sehingga,
Fungsi kuadrat yang akan dicari memotong sumbu-y pada y = 2, atau dengan kata lain memotong sumbu-y di titik (0, 2). Sehingga,

Setelah itu kita substitusikan titik (–1, 6) pada persamaan.

Persamaan yang diperoleh ini dimisalkan dengan persamaan 1.
Lanjut ke titik (2, 12). Apabila titik (2, 12) disubstitusikan ke bentuk umum fungsi kuadrat, akan menjadi seperti berikut.

Persamaan yang diperoleh ini dimisalkan dengan persamaan 2.
Selanjutnya, lakukan metode eliminasi persamaan 2 terhadap persamaan 1 dengan menghilangkan/mengeliminasi variabel b.

Sehingga diperoleh a = 3. Substitusikan hasil ini ke persamaan 1 atau 2. Apabila a = 3 disubstitusikan ke persamaan 1, maka 3 – b = 4. Diperoleh b = 3 – 4 = –1. Jadi, fungsi kuadrat yang melalui titik-titik (–1, 6) dan (2, 12) serta memotong sumbu-y pada y = 2 adalah f(x) = 3x2 – x + 2.
Fungsi kuadrat yang melalui titik-titik (–1, 6) dan (2, 12) serta memotong sumbu-y pada y = 2 adalah f(x) = 3x2 – x + 2.
Untuk meyakinkan akan kebenaran jawaban ini, mari kita uji fungsi kuadrat ini dengan titik-titik (–1, 6), (2, 12), dan (0, 2).

Pada perhitungan di atas dapat diperoleh bahwa untuk x = –1 diperoleh y = 6, untuk x = 2 diperoleh y = 12, dan untuk x = 0 diperoleh y = 2. Sehingga fungsi f(x) = 3x2 – x + 2 memotong titik-titik (–1, 6), (2, 12), dan (0, 2). Sesuai yang diminta soal. Jadi, dari hasil ini dapat disimpulkan bahwa pekerjaan kita dalam menyusun fungsi kuadrat di atas benar.
No comments:
Post a Comment