Penyelesaian Persamaan Kuadrat dengan Sifat Akar Persamaan

Selamat datang, Kali ini kita akan berbagi tentang Penyelesaian Persamaan Kuadrat dengan Sifat Akar Persamaan. Silahkan dibaca baik-baik tentang Penyelesaian Persamaan Kuadrat dengan Sifat Akar Persamaan ini ya.

Persamaan x2 = 25 dapat diselesaikan dengan menggunakan pemfaktoran. Bentuk standar dari x2 = 25 adalah x2 – 25 = 0 yang dapat difaktorkan menjadi (x – 5)(x + 5) = 0. Sehingga, solusi-solusi dari persamaan kuadrat tersebut adalah x = 5 atau x = –5, yang merupakan bilangan positif dan negatif dari akar kuadrat 25. Hasil ini memberikan suatu metode untuk menyelesaikan suatu persamaan kuadrat yang berbentuk X2 = k, yang selanjutnya disebut sifat akar kuadrat dari suatu persamaan.

Sifat Akar Kuadrat dari Suatu Persamaan
Jika X merepresentasikan suatu bentuk aljabar dan X2 = k, maka X = √k atau X = –√k, atau juga dapat dituliskan X = ±√k

Untuk lebih memahami penggunaan metode ini dalam menyelesaikan persamaan kuadrat, perhatikan contoh soal berikut.

Contoh 3: Penggunaan Sifat Akar Kuadrat dari Suatu Persamaan

Gunakan sifat akar kuadrat dari suatu persamaan untuk menyelesaikan masing-masing persamaan berikut.

1. –9x2 + 12 = –13
2. x2 – 18 = 0
3. (x + 1)2 = 36

Pembahasan

1. Persamaan –9x2 + 12 = –13 tidak berbentuk X2 = k. Sehingga kita harus mengubah persamaan kuadrat tersebut menjadi bentuk seperti itu.
   
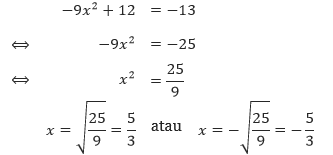
   Sehingga, selesaian dari persamaan –9x2 + 12 = –13 adalah x = 5/3 atau x = –5/3.
2. Bentuk X2 = k dari x2 – 18 = 0 adalah x2 = 18. Sehingga,
   
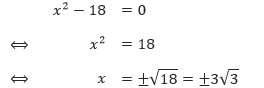
   Jadi, selesaian dari persamaan x2 – 18 = 0 adalah x = 3√3 atau x = –3√3.
3. Persamaan (x + 1)2 = 36 sudah memiliki bentuk X2 = k. Sehingga,
   
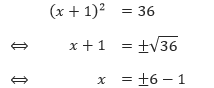
   Sehingga, selesaian dari persamaan (x + 1)2 = 36 adalah x = 6 – 1 = 5 atau x = –6 – 1 = –7.

Untuk persamaan yang berbentuk (ax + b)2 = k (seperti contoh 3), dapat juga diselesaikan dengan menggunakan pemfaktoran. Akan tetapi kita harus menulis pangkat dua binomial tersebut ke dalam ekspansi/bentuk panjangnya, kemudian menyederhanakan persamaan yang diperoleh agar ruas kanan sama dengan nol dan terakhir, kita dapat memfaktorkan persamaan tersebut untuk menentukan selesaian-selesaiannya. Dengan menggunakan sifat akar kuadrat dari suatu persamaan, kita dapat menyelesaikan persamaan yang berbentuk (ax + b)2 = k secara lebih mudah.

Semoga postingan kami tentang Penyelesaian Persamaan Kuadrat dengan Sifat Akar Persamaan ini bisa bermanfaat dan menambah pengetahuan serta pemahaman matematika kamu. Jangan lupa tetap Berbagi Belajar,Belajar Berbagi.
    dalam: Kelas 10

Share Yuk

   

Postingan Terkait