Cara Menentukan Nilai Optimum Program Linear dengan Metode Titik Pojok

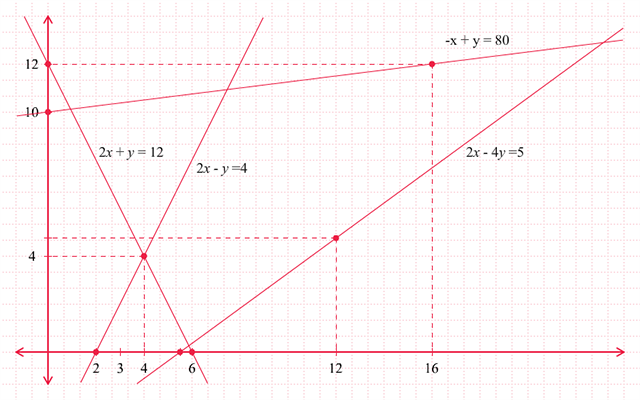
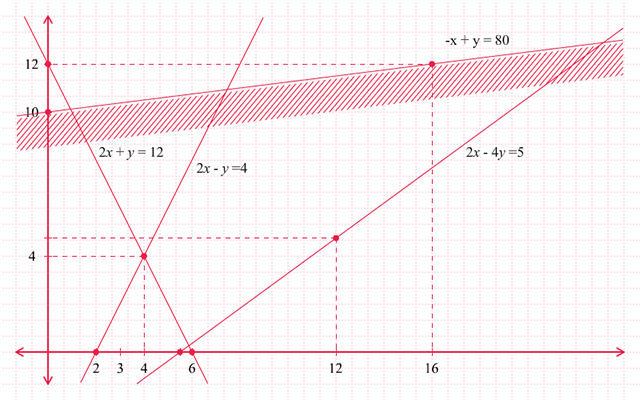
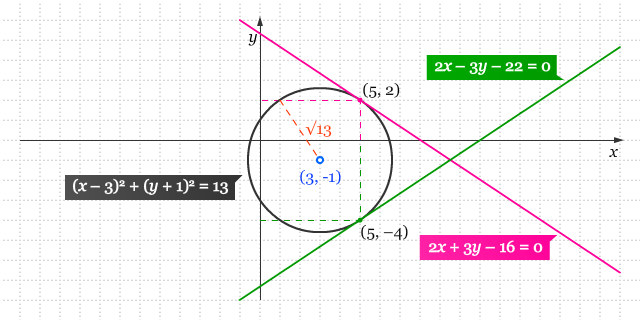
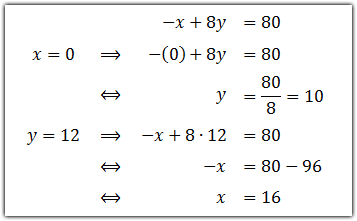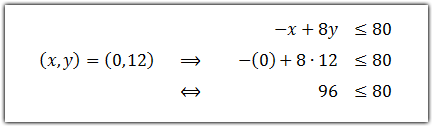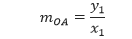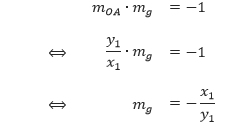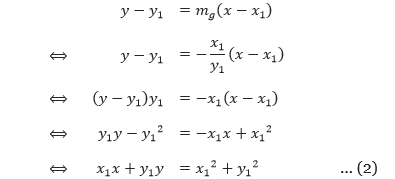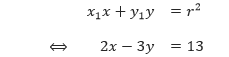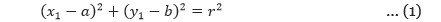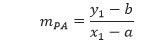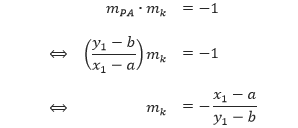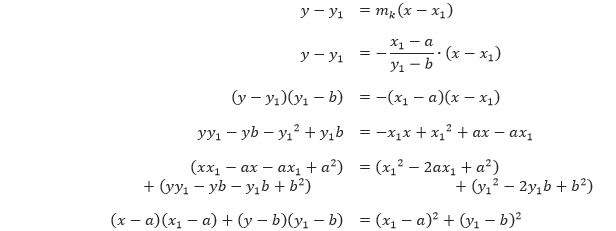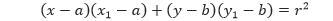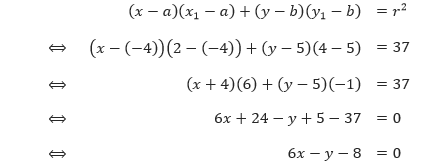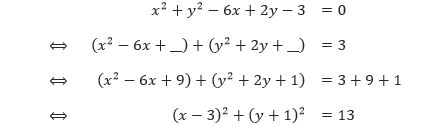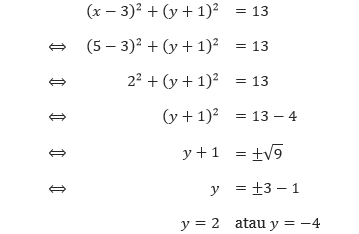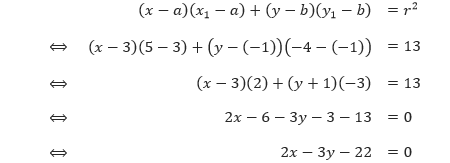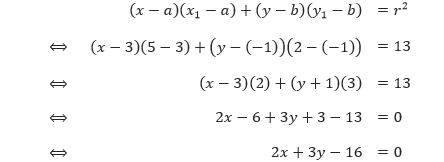x + y ≤ 600,
6.000x + 5.000y ≤ 600.000,
Untuk x, y anggota bilangan cacah, x ≥ 0, y ≥ 0

Dari sistem pertidaksamaan tersebut akan dicari nilai-nilai x dan y yang menyebabkan fungsi f(x,y) = 500x + 600y bernilai maksimum. Bentuk umum dari fungsi tersebut adalah f(x, y) = ax + by. Fungsi yang akan dioptimumkan (maksimum atau minimum) ini kemudian disebut fungsi objektif. Untuk menentukan nilai optimum tersebut, dapat digunakan metode uji titik pojok.

Sebelum membahas metode uji titik pojok, sebaiknya kalian tahu mengenai nilai optimum. Nilai optimum dapat berupa nilai maksimum atau minimum, tergantung dari permintaan soal. Pada permasalahan ini yang diminta adalah nilai maksimum, sehingga kita akan mencari nilai-nilai x dan y yang menyebabkan fungsi objektif bernilai maksimum.

Metode Uji Titik Pojok

Untuk menentukan nilai optimum dengan menggunakan metode uji titik pojok, lakukan langkah-langkah berikut.

1. Tentukan kendala-kendala dari permasalahan program linear yang dimaksud.
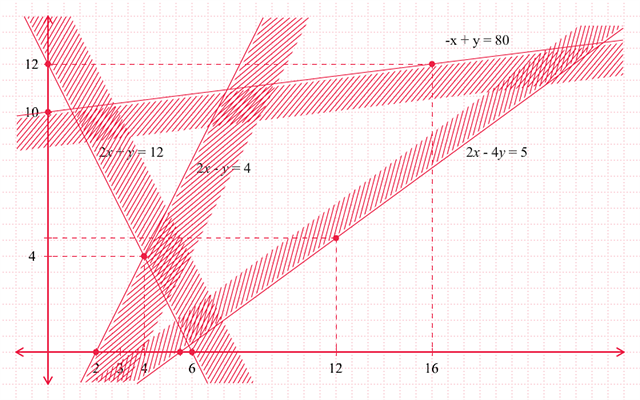
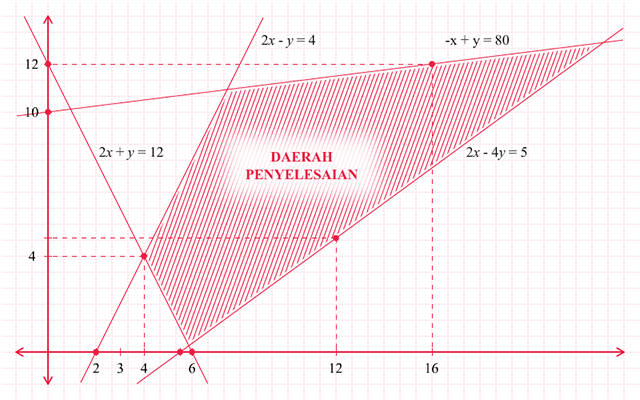
2. Gambarlah daerah penyelesaian dari kendala-kendala dalam masalah program linear tersebut.
3. Tentukan titik-titik pojok dari daerah penyelesaian itu.
4. Substitusikan koordinat setiap titik pojok itu ke dalam fungsi objektif.
5. Bandingkan nilai-nilai fungsi objektif tersebut. Nilai terbesar berarti menunjukkan nilai maksimum dari fungsi f(x, y), sedangkan nilai terkecil berarti menunjukkan nilai minimum dari fungsi f(x, y).

Untuk lebih memahami dalam menentukan nilai optimum suatu fungsi objektif dengan menggunakan metode uji pojok, perhatikan contoh soal berikut.

Contoh Soal

Ling ling membeli 240 ton beras untuk dijual lagi. Ia menyewa dua jenis truk untuk mengangkut beras tersebut. Truk jenis A memiliki kapasitas 6 ton dan truk jenis B memiliki kapasitas 4 ton. Sewa tiap truk jenis A adalah Rp 100.000,00 sekali jalan dan truk jenis B adalah Rp 50.000,00 sekali jalan. Maka Ling ling menyewa truk itu sekurang-kurangnya 48 buah. Berapa banyak jenis truk A dan B yang harus disewa agar biaya yang
dikeluarkan minimum?

Pembahasan Contoh Soal

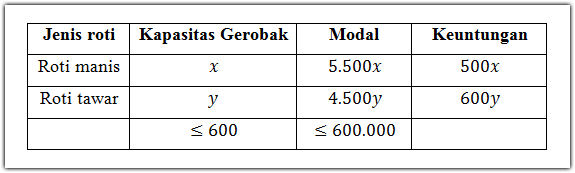
Langkah pertama. Tentukan kendala-kendala dari permasalahan program linear yang dimaksud oleh soal. Untuk mengetahui kendala-kendalanya, sebaiknya kita ubah soal tersebut ke dalam tabel sebagai berikut.

Sehingga, kendala-kendalanya dapat dituliskan sebagai berikut.

x + y ≥ 48,
6x + 4y ≥ 240,
x ≥ 0, y ≥ 0, x, y anggota bilangan cacah

Dengan fungsi objektifnya adalah f(x, y) = 100.000x + 50.000y.

Langkah kedua. Gambarkan daerah penyelesaian dari kendala-kendala di atas. Gambar dari daerah penyelesaian sistem pertidaksamaan di atas adalah sebagai berikut (baca: “Program Linear: Menggambar Daerah Penyelesaian Sistem Pertidaksamaan Linear Dua Variabel”).

Langkah ketiga. Tentukan titik-titik pojok dari daerah penyelesaian itu. Titik pojok dari daerah penyelesaian di atas adalah titik potong garis 6x + 4y = 240 dengan sumbu-y, titik potong garis x + y = 48 dengan sumbu-x, dan titik potong garis-garis x + y = 48 dan 6x + 4y = 240.

Titik potong garis 6x + 4y = 240 dengan sumbu-y adalah titik (0, 60). Titik potong garis x+ y = 48 dengan sumbu-x adalah titik (48, 0). Sedangkan titik potong garis-garis x + y = 48 dan 6x + 4y = 240 dapat dicari dengan menggunakan cara eliminasi berikut ini.

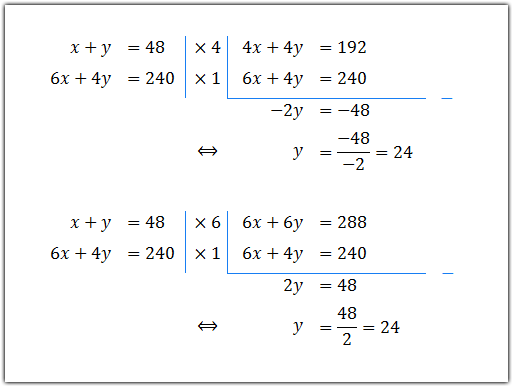
Diperoleh, titik potong garis-garis x + y = 48 dan 6x + 4y = 240 adalah pada titik (24, 24).

Langkah keempat. Substitusikan koordinat setiap titik pojok itu ke dalam fungsi objektif.

Langkah kelima. Bandingkan nilai-nilai fungsi objektif tersebut. Dari ketiga hasil tersebut, dapat diperoleh bahwa agar biaya yang dikeluarkan minimum, Ling ling harus menyewa 60 truk jenis B dan tidak menyewa truk jenis A.

Baca Juga Cara Menentukan Nilai Optimum Program Linear dengan Metode Garis Selidik

Program Linear: Menggambar Daerah Penyelesaian Sistem Pertidaksamaan Linear Dua Variabel

Sistem pertidaksamaan linear dua variabel berupa beberapa pertidaksamaan linear yang terdiri dari 2 variabel, biasanya x atau y (walaupun jenis variabel lainnya tetap memungkinkan). Pertidaksamaan linear dua variabel memiliki bentuk umum seperti berikut:

ax + by < c, ax + by > c, ax + by ≤ c, atau ax + by ≥ c

Sebelum menggambar daerah penyelesaian sistem pertidaksamaan linear dua variabel, sebaiknya kita tahu terlebih dahulu mengenai himpunan penyelesaian. Himpunan penyelesaian merupakan himpunan pengganti nilai variabel sedemikian sehingga menyebabkan sistem pertidaksamaan menjadi pernyataan yang benar. Daerah penyelesaian yang akan kita gambar merupakan daerah dari himpunan penyelesaian tersebut. Daerah ini berisi himpunan pasangan berurutan (x, y) yang menjadi anggota dari himpunan penyelesaian.

Untuk menggambar daerah penyelesaian sistem pertidaksamaan linear dua variabel, perhatikan contoh soal berikut.

Contoh Soal

Gambarlah daerah penyelesaian dari sistem pertidaksamaan linear berikut untuk x, yanggota bilangan real.

–x + 8y ≤ 80
2x – 4y ≤ 5
2x + y ≥ 12
2x – y ≥ 4
x ≥ 0, y ≥ 0

Pembahasan Contoh Soal

Untuk menggambar daerah penyelesaian dari sitem pertidaksamaan yang dimaksud, lakukan langkah-langkah berikut:

Langkah pertama. Ubahlah pertidaksamaan-pertidaksamaan yang dimaksud menjadi persamaan linear, kemudian gambarkan persamaan linear tersebut pada bidang koordinat. Grafik dari persamaan linear berupa garis lurus. Untuk itu, cari dua titik yang dilewati oleh garis tersebut, kemudian hubungkan kedua titik tersebut menjadi suatu garis lurus. Dua titik ini biasanya dipilih titik pada sumbu-x dan sumbu-y, akan tetapi apabila kurang memungkinkan, pilihlah titik-titik lain.

Sehingga garis –x + 8y = 80 melalui titik-titik (0, 10) dan (16, 12). Dengan cara yang sama, dapat dicari 2 titik yang dilalui persamaan garis lainnya.

Sehingga, garis-garis dari –x + 4y = 80, 2x – 4y = 5, 2x + y = 12, dan 2x – y = 4 dapat digambarkan seperti berikut.

Langkah kedua. Arsirlah daerah dari masing-masing pertidaksamaan. Untuk menentukan daerah pertidaksamaan, pilihlah salah satu titik yang terdapat di kanan atau di kiri, atas atau bawah dari garis. Apabila koordinat titik tersebut disubstitusikan ke dalam pertidaksamaan dan menghasilkan pernyataan yang benar, maka daerah titik tersebut merupakan daerah penyelesaian pertidaksamaan tersebut. Arsirlah daerah penyelesaian tersebut. Sebaliknya, apabila koordinat titik tersebut disubstitusikan ke dalam pertidaksamaan dan menghasilkan pernyataan yang salah, maka daerah titik tersebut bukan merupakan daerah penyelesaian pertidaksamaan tersebut. Arsirlah daerah yang berseberangan terhadap titik tersebut. Misalkan kita akan menemukan daerah penyelesaian dari pertidaksamaan –x + 8y ≤ 80. Misalkan kita pilih titik (0, 12) yang terletak di atas garis sebagai titik uji. Kita substitusikan ke dalam pertidaksamaan sebagai berikut.

Dengan mensubstitusikan titik (0, 12) ke pertidaksamaan –x + 8y ≤ 80 menghasilkan pernyataan yang salah, sehingga daerah yang memuat titik (0, 12) bukan penyelesaian dari pertidaksamaan tersebut. Sehingga daerah yang berlawanan dengan daerah tersebut, yaitu daerah bawah, yang kita arsir.

Dengan cara yang sama, kita cari daerah penyelesaian dari pertidaksamaan-pertidaksamaan lainnya. Setelah itu kita gambarkan daerahnya seperti pada gambar berikut.

Langkah ketiga. Arsirlah daerah himpunan penyelesaian dari sistem pertidaksamaan yang dimaksud. Himpunan penyelesaian dari sistem pertidaksamaan merupakan irisan dari himpunan penyelesaian dari masing-masing pertidaksamaan. Atau secara visual, daerah penyelesaian dari sistem pertidaksamaan merupakan daerah yang terkena arsiran dari semua daerah penyelesaian. Sehingga himpunan penyelesaian dari pertidaksamaan –x + 8y ≤ 80, 2x – 4y ≤ 5, 2x + y ≥ 12, 2x – y ≥ 4, x ≥ 0, dan y ≥ 0 dapat digambarkan sebagai berikut.

Menyusun Model Matematika dalam Program Linear

Pertidaksamaan linear dapat digunakan untuk memecahkan masalah dalam kehidupan sehari-hari. Hal ini dapat dilakukan dengan memodelkan masalah tersebut ke dalammodel matematika. Sebagai contoh perhatikan permasalahan berikut ini.

Pak Budi adalah seorang pedagang roti. Beliau menjual roti menggunakan gerobak yang hanya dapat memuat 600 roti. Roti yang dijualnya adalah roti manis dan roti tawar dengan harga masing-masing adalah Rp 5.500,00 dan Rp 4.500,00 per bungkusnya. Dari penjualan roti ini, beliau memperoleh keuntungan Rp 500,00 dari sebungkus roti manis dan Rp 600,00 dari sebungkus roti tawar. Apabila modal yang dimiliki oleh Pak Budi adalah Rp 600.000, buatlah model matematika dengan tujuan untuk memperoleh keuntungan sebesar-besarnya!

Permasalah di atas dapat dimodelkan dalam bentuk matematika dengan menggunakan sistem pertidaksamaan linear dua variabel. Dengan memisalkan banyaknya roti manis dan roti tawar secara berturut-turut sebagai x dan y, maka diperoleh tabel sebagai berikut.

Sehingga apabila dituliskan dalam bentuk sistem pertidaksamaan akan menjadi seperti berikut ini.

x + y ≤ 600,
5.500x + 4.500y ≤ 600.000,
Untuk x, y anggota bilangan cacah, x ≥ 0, y ≥ 0

Dua pertidaksamaan yang terakhir (baris ketiga) menunjukkan syarat dari nilai x dan y. Karena x dan y secara berturut-turut menyatakan banyaknya roti, maka tidak mungkin nilai x dan y bernilai negatif.

Perhatikan kolom keempat dari tabel di atas. Kolom keempat tersebut menyatakan fungsi yang akan ditentukan nilai maksimumnya (nilai optimum). Fungsi tersebut dapat dituliskan dalam persamaan matematika sebagai berikut.

f(x,y) = 500x + 600y

Tujuan dari permasalahan ini adalah mencari nilai x dan y yang menjadi anggota himpunan penyelesaian dari sistem pertidaksamaan, serta membut fungsi f(x,y) = 500x + 600y bernilai optimum (maksimum).

Ya, kita telah berhasil merumuskan masalah di atas ke dalam suatu model matematika. Dari ilustrasi di atas, dapatkah kalian menyimpulkan pengertian dari model matematika?

Model matematika adalah suatu cara sederhana untuk menerjemahkan suatu masalah ke dalam bahasa matematika dengan menggunakan persamaan, pertidaksamaan, atau fungsi.

Contoh Soal dan Pembahasan Permutasi

Misalkan diberikan suatu himpunan {a, b, c}. Dari anggota-anggota himpunan-himpunan tersebut dapat disusun kata sebagai berikut: abc, acb, bac, bca, cab, dan cba. Susunan ketiga anggota himpunan itu disebut permutasi dari a, b, dan c. (Perhatikan bahwa masing-masing susunan mempunyai urutan yang berbeda dari a, b, dan c).

Dari himpunan tersebut dapat juga dibentuk susunan-susunan yang masing-masing terdiri dari dua unsur yang berbeda dengan urutan: ab, ba, ac, ca, bc, dan cb. Susunan kedua anggota himpunan itu masing-masing disebut permutasi dari a, b, dan c.

Secara umum dapat dikatakan bahwa,

Permutasi dari sekumpulan objek adalah susunan yang berbeda dari objek-objek itu dengan memperhatikan urutannya.

Permutasi pada contoh pertama disebut permutasi tiga-tiga dari 3 objek dilambangkan dengan 3P3, sedangkan permutasi pada contoh kedua disebut permutasi dua-dua dari 3 objek dilambangkan dengan 3P2. Banyaknya permutasi dari n objek yang disusun r objek, dinotasikan dengan nPr, dapat dirumuskan sebagai berikut.

Untuk membuktikan rumus tersebut, perhatikan uraian berikut ini.

Permutasi dapat diartikan dengan susunan berbeda (tanpa pengulangan) yang dapat dibentuk dari n objek yang disediakan, untuk mengisi r kotak. Untuk tempat pertama dalam permutasi itu dapat diambil setiap objek dari n objek yang ada, jadi ada n cara. Tempat kedua dapat ditempati setiap objek kecuali satu unsur yang telah dipakai untuk tempat pertama, jadi ada (n – 1) cara. Untuk tempat ketiga terdapat (n – 2) cara, tempat keempat ada (n – 3) cara, dan seterusnya. Sehingga untuk tempat ke-r terdapat (n – r +1) cara. Menurut prinsip perkalian, akan terdapat n(n – 1)(n – 2) … (n – r + 1) cara. Jadi, nPr = n(n – 1)(n – 2) … (n – r + 1) atau

Untuk n = r diperoleh,

Untuk mengetaui bagaimana permutasi digunakan dalam pemecahan masalah, perhatikan contoh soal berikut.

Contoh Soal

Terdapat 3 anak laki-laki dan 4 orang anak perempuan.

1. Dengan berapa cara mereka dapat duduk berdampingan?
2. Dengan berapa cara mereka dapat duduk berdampingan, jika anak laki-laki dan perempuan masing-masing mengelompok sehingga hanya sepasang anak laki-laki dan perempuan yang berdampingan?

Pembahasan Contoh Soal

Berikut ini pembahasan dari masing-masing soal di atas.

1. Banyaknya cara mereka agar dapat duduk berdampingan dapat dicari dengan menggunakan permutasi, yaitu 7P7 = 7! = 5.040. Mengapa kita menggunakan 7P7? Perhatikan bahwa bahwa terdapat 4 anak laki-laki dan 3 anak perempuan, sehingga totalnya ada (4 + 3), yaitu 7 anak yang akan disusun untuk duduk berdampingan. Tentunya terdapat 7 kursi untuk membuat mereka duduk saling berdampingan. Terdapat 7 objek akan disusun pada 7 tempat, hal ini sama dengan 7P7.
2. Untuk membantu dalam memahami soal poin (b), perhatikan gambar berikut.
   
   Seperti yang diilustrasikan pada gambar, agar 3 anak laki dapat selalu duduk mengelompok, kita dapat membendel 3 anak tersebut menjadi satu. Demikian juga dengan 4 anak perempuan. Sehingga kita akan menyusun 2 bendel pada 2 tempat yang disediakan, 2P2. Bendel pertama terdiri dari 3 anak laki-laki. Tiga anak laki-laki ini disusun pada 3 tempat, 3P3. Bendel kedua terdiri dari 4 anak perempuan. Empat anak perempuan ini disusun pada 4 tempat, 4P4. Sehingga, banyaknya cara menyususun 3 anak laki-laki dan 4 anak perempuan agar anak laki-laki dan perempuan saling mengelompok adalah
   
   Jadi, terdapat 288 cara penyusunan yang memenuhi syarat poin (b).

Cara Menggambar Lingkaran dari Persamaan yang Diketahui

Grafik dari suatu lingkaran dapat ditentukan apabila kita mengetahui titik pusat dan jari-jari lingkaran tersebut. Untuk mengetahui titik pusat dan jari-jari lingkaran tersebut, kita harus menuliskan persamaan lingkaran tersebut ke dalam persamaan lingkaran standar. Setelah titik pusat diketahui, kita dapat menentukan titik-titik yang berjarak r satuan di sebelah kanan, kiri, atas, dan bawah dari titik pusat tersebut. Sehingga kita memperoleh 4 titik yang dapat digunakan untuk melukis grafik lingkaran yang diminta. Perhatikan contoh 1 berikut.

Contoh 1: Melukis Grafik Persamaan Lingkaran

Lukislah grafik lingkaran yang memiliki persamaan (x – 2)2 + (y + 3)2 = 12. Labelilah titik pusat dan jari-jarinya secara jelas.

Pembahasan Karena lingkaran dengan persamaan (x – a)2 + (y – b)2 = r2 memiliki titik pusat di (a, b) dan jari-jari r, maka dari persamaan (x – 2)2 + (y + 3)2 = 12 kita dapat memperoleh a = 2, b = –3, dan r = √12 = 2√3.

Sehingga, lingkaran tersebut memiliki titik pusat di (2, –3) dan jari-jari r ≈ 3,5 satuan. Selanjutnya, plotlah titik pusat (2, –3) kemudian plotlah 4 titik yang berjarak kira-kira 3,5 satuan ke arah vertikal dan horizontal dari titik pusat tersebut. Hubungkan keempat titik tersebut dengan lingkaran.

Pada contoh 1 di atas, persamaan lingkaran dinyatakan dalam bentuk kuadrat dari binomial pada variabel x dan y. Dengan mengekspansi binomial-binomial tersebut dan mengkombinasikan suku-suku sejenis, kita dapat menuliskan bentuk umum dari persamaan lingkaran tersebut:

Dari bentuk umum persamaan lingkaran di atas, kita dapat mengamati bahwa persamaan tersebut terdiri dari penjumlahan variabel x dan y yang berderajat 2 dan koefisiennya sama (dalam kasus ini koefisiennya 1).

Karena persamaan ini diperoleh dari mengkuadratkan binomial, kita juga dapat mengubah persamaan umum lingkaran tersebut kembali ke dalam bentuk kuadrat dari binomial. Untuk alasan ini, kita dapat menggunakan teknik melengkapkan kuadrat.

Contoh 2: Menentukan Titik Pusat dan Jari-jari dari Suatu Lingkaran

Tentukan titik pusat dan jari-jari lingkaran yang memiliki persamaan x2 + y2 + 2x – 4y – 4 = 0. Kemudian lukislah grafik dari lingkaran tersebut.

Pembahasan Untuk menentukan titik pusat dan jari-jarinya, kita harus melengkapkan kuadrat dari kedua variabel x dan y.

Sehingga dari persamaan (x + 1)2 + (x – 2)2 = 9, kita dapat dengan mudah mengetahui bahwa lingkaran tersebut memiliki titik pusat di (–1, 2) dan jari-jari r = 3. Grafik dari lingkaran tersebut dapat ditunjukkan seperti berikut.

Contoh 3: Penerapan Persamaan Suatu Lingkaran

Untuk membantu dalam penelitian hewan yang aktif pada malam hari, beberapa ahli binatang memasang detektor gerak di dekat lubang saluran air. Alat ini memiliki jangkauan 10 m ke berbagai arah. Andaikan lubang air tersebut memiliki koordinat (0, 0) dan alat itu dipasang pada koordinat (2, –1).

1. Tulislah persamaan lingkaran yang memodelkan jangkauan maksimum dari alat tersebut.
2. Gunakan rumus jarak untuk menentukan apakah alat tersebut dapat mendeteksi seekor luwak yang sedang mendekati lubang air dan sekarang koordinatnya ada di (11, –5).

Pembahasan

1. Karena alat detektor tersebut berada pada koordinat (2, –1) dan memiliki jangkauan r= 10 m, setiap pergerakan di dalam lingkaran yang memiliki persamaan (x – 2)2 + (y + 1)2 = 100 bisa terdeteksi.
2. Dengan menggunakan titik-titik (2, –1) dan (11, –5) pada rumus jarak, akan menghasilkan
   
   Karena 9,85 < 10, luwak tersebut akan terdeteksi oleh alat tersebut.

Dan akhirnya, pada pembahasan ini kita telah bisa menggambar grafik dari persamaan lingkaran. Apabila persamaan lingkaran tersebut berbentuk x2 + y2 + Ax + By + C = 0, kita perlu mengubahnya ke dalam persamaan yang berbentuk (x – a)2 + (y – b)2 = r2 agar kita dapat menentukan letak titik pusat dan jari-jarinya

Persamaan Garis Singgung Lingkaran

Sebelum menentukan persamaan garis singgung lingkaran, ada baiknya kita mengingat kembali mengenai sifat-sifat garis singgung lingkaran. Garis singgung lingkaran merupakan garis yang menyinggung suatu lingkaran. Kata kunci dari definisi tersebut adalah “menyinggung”. Apabila suatu garis menyinggung lingkaran, maka garis tersebut tepat melalui satu titik pada lingkaran. Perhatikan beberapa kedudukan garis terhadap lingkaran berikut.

Berdasarkan gambar di atas, kita dapat melihat bahwa garis k tidak memotong lingkaranO, garis l menyinggung lingkaran O di titik A, dan garis m memotong lingkaran O di titik-titik B dan C. Karena suatu garis singgung tepat melalui satu titik pada lingkaran (misalkan titik A), maka garis singgung tersebut akan tegak lurus dengan jari-jari lingkaran yang menghubungkan titik A dengan titik pusat lingkaran. Sifat dari garis singgung tersebut dapat digunakan untuk menentukan persamaan garis singgung lingkaran.

Menentukan Persamaan Garis Singgung

Pada bagian ini kita akan menentukan persamaan garis singgung yang melalui titik A(x1,y1) pada lingkaran yang memiliki persamaan x2 + y2 = r2, yaitu lingkaran yang berpusat di titik (0, 0) dan berjari-jari r. Perhatikan ilustrasi berikut.

Misalkan kita akan menentukan persamaan garis g yang melalui titik A(x1, y1), yaitu titik pada lingkaran x2 + y2 = r2. Karena titik A(x1, y1) terletak pada lingkaran x2 + y2 = r2 maka,

Selanjutnya kita buat ruas garis OA, yaitu ruas garis yang memiliki ujung-ujung di titik O(pusat lingkaran) dan titik A. Sehingga gradien dari ruas garis tersebut adalah

Karena garis g tegak lurus dengan ruas garis OA, maka

Karena garis g melalui titik A(x1, y1) dan bergradien mg = –x1/y1, maka persamaan garis gdapat ditentukan sebagai berikut.

Dengan mensubstitusi persamaan (1) ke persamaan (2) diperoleh x1x + y1y = r2. Sehingga, persamaan garis singgung yang melalui satu titik pada lingkaran x2 + y2 = r2 dapat disimpulkan sebagai berikut.

Persamaan Garis Singgung Lingkaran
Persamaan garis singgung yang melalui titik A(x1, y1) pada lingkaran x2 + y2 = r2 adalah x1x + y1y = r2.

Untuk lebih memahami mengenai persamaan garis singgung lingkaran, perhatikan contoh berikut.

Contoh: Menentukan Persamaan Garis Singgung

Tentukan persamaan garis singgung yang melalui titik (2, –3) pada lingkaran x2 + y2 = 13.

Pembahasan Dengan (x1, y1) = =(2, –3) dan x2 + y2 = 13, kita mendapatkan x1 = 2, y1 = –3, dan r2 = 13. Sehingga persamaan garis singgung tersebut adalah

Berikutnya,

kita akan menentukan persamaan garis singgung lingkaran yang melalui titik A(x1, y1) pada lingkaran yang berpusat di titik (a, b) dan berjari-jari r. Seperti kita ketahui, persamaan lingkaran yang berpusat di titik (a, b) dan berjari-jari r adalah (x– a)2 + (y – b)2 = r2. Karena titik (x1, y1) terletak pada lingkaran maka,

Untuk mengetahui ilustrasi mengenai letak garis singgung terhadap lingkaran tersebut, perhatikan ilustrasi berikut.

Apabila kita membuat ruas garis PA, yaitu jari-jari dari lingkaran P, maka gradien dari ruas garis tersebut adalah

Karena ruas garis PA merupakan jari-jari yang memiliki salah satu titik ujung di titik A, yaitu titik yang juga dilalui oleh garis singgung k, maka ruas garis PA tegak lurus dengan garis k. Hal ini mengakibatkan,

Karena garis k melalui titik A(x1, y1) dan bergradien mk = –(x1 – a)/(y1 – b), maka persamaan garis k adalah

Apabila kita mensubstitusikan persamaan (1) ke dalam persamaan di atas, maka kita akan memperoleh,

Sehingga, dari penghitungan di atas kita dapat menyimpulkan persamaan garis singgung yang kita peroleh adalah sebagai berikut.

Persamaan Garis Singgung Lingkaran
Persamaan garis singgung lingkaran yang melalui titik (x1, x2) pada lingkaran (x – a)2 + (y – b)2 = r2 adalah,
(x – a)(x1 – a) + (y – b)(y1 – b) = r2.

Selanjutnya, perhatikan contoh permasalahan mengenai garis singgung lingkaran (x – a)2+ (y – b)2 = r2 berikut.

Contoh 1: Persamaan Garis Singgung Lingkaran

Tentukan persamaan garis singgung di titik (2, 4) pada lingkaran (x + 4)2 + (y – 5)2 = 37.

Pembahasan Lingkaran yang memiliki persamaan (x + 4)2 + (y – 5)2 = 37 memiliki titik pusat di (a, b) = (–4, 5) dan kuadrat jari-jarinya, r2 = 37. Sehingga persamaan garis singgung yang melalui titik (x1, y1) = (2, 4) pada lingkaran tersebut adalah

Sehingga, persamaan garis singgung lingkaran tersebut adalah 6x – y – 8 = 0.

Selanjutnya bagaimana kalau persamaan lingkarannya tidak ditulis ke dalam bentuk (x –a)2 + (y – b)2 = r2, tetapi ke dalam bentuk persamaan umum lingkaran. Perhatikan contoh soal selanjutnya berikut.

Contoh 2: Garis Singgung untuk x2 + y2 + Ax + By + C = 0

Carilah persamaan garis singgung pada lingkaran x2 + y2 – 6x + 2y – 3 = 0 di titik yang berabsis 5.

Pembahasan Pertama, kita ubah persamaan x2 + y2 – 6x + 2y – 3 = 0 menjadi bentuk (x– a)2 + (y – b)2 = r2.

Sehingga, lingkaran tersebut memiliki titik pusat di (a, b) = (3, –1) dan kudrat dari jari-jarinya r2 = 13. Selanjutnya kita tentukan titik pada lingkaran tersebut yang berabsis 5. Untuk x = 5, kita memperoleh

Sehingga, titik-titik pada lingkaran tersebut yang berabsis 5 adalah (5, –4) dan (5, 2). Diperoleh, persamaan garis singgung yang melalui titik (5, –3) adalah

Sedangkan persamaan garis singgung yang melalui titik (5, 2) adalah

Jadi, persamaan garis-garis singgungnya adalah 2x – 3y – 22 = 0 dan 2x + 3y – 16 = 0. Perhatikan gambar dari dua garis singgung tersebut.