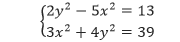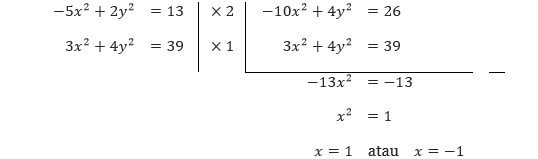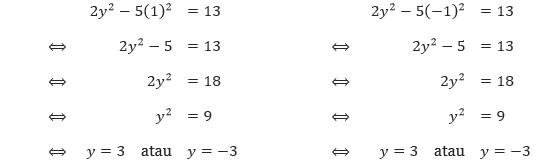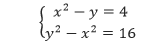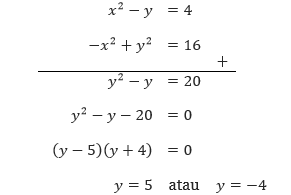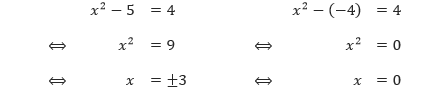Soal dan Pembahasan Jaring Jaring Limas

Lihat Materi Jaring Jaring Limas

Lukislah jaring-jaring limas segi empat apabila diketahui sisi alas dan proyeksi titik puncak pada bidang alasnya seperti berikut!

Pembahasan

Jaring-jaring dari limas yang dimaksud adalah seperti berikut.

Soal dan Pembahasan Sistem Persamaan non-Linear dan Irisan Kerucut

Seperti dalam sistem persamaan linear dua variabel (SPLDV) ataupun sistem persamaan linear tiga variabel (SPLTV), metode substitusi, eliminasi, dan grafik dapat digunakan untuk menyelesaikan sistem yang memuat persamaan-persamaan dalam keluarga irisan kerucut. Jika kedua persamaan dalam sistem tersebut memuat paling sedikit satu suku yang berderajat dua, akan lebih mudah jika sistem tersebut diselesaikan dengan metode eliminasi.

Contoh 1: Menyelesaikan Sistem Persamaan Nonlinear

Selesaikan sistem berikut dengan menggunakan metode eliminasi:

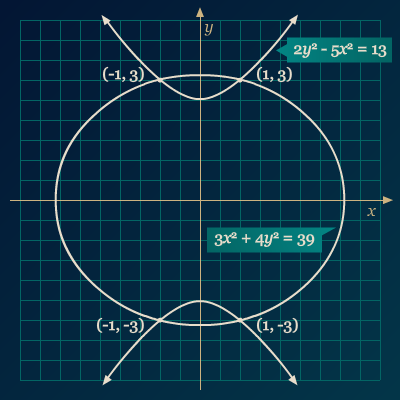
Pembahasan Persamaan pertama merupakan suatu persamaan dari hiperbola vertikal yang memiliki titik pusat di (0, 0), sedangkan persamaan kedua merupakan suatu persamaan elips horizontal yang berpusat di (0, 0). Dengan mengeliminasi suku-y pada kedua persamaan, kita peroleh

Dengan mensubstitusikan x = 1 dan x = –1 pada persamaan pertama, kita mendapatkan

Karena masing-masing 1 dan –1 menghasilkan dua nilai y, maka selesaian dari sistem persamaan tersebut terdiri dari 4 pasangan berurutan, yaitu (1, 3), (1, –3), (–1, 3), dan (–1, –3). Grafik dari sistem persamaan tersebut dapat ditunjukkan sebagai berikut.

Contoh 2: Titik Potong Dua Grafik

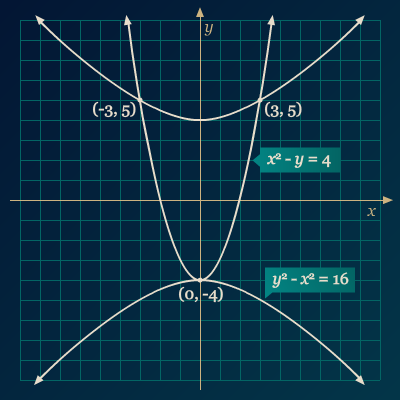
Tentukan titik potong dua grafik yang dibentuk oleh persamaan-persamaan x2 – y = 4 dany2 – x2 = 16.

Pembahasan Untuk menentukan titik potong dua grafik, kita terlebih dahulu harus menyelesaikan sistem persamaan nonlinear berikut.

Persamaan pertama tersebut merupakan persamaan dari suatu parabola vertikal, sedangkan persamaan kedua merepresentasikan suatu hiperbola vertikal yang memiliki titik pusat di (0, 0). Dengan mengeliminasi suku yang memuat variabel x pada kedua persamaan, kita mendapatkan

Dengan mensubstitusikan y = 5 dan y = –4 ke dalam persamaan pertama, diperoleh

Dengan mensubstitusikan y = 5 diperoleh dua nilai x, sedangkan dengan mensubstitusikan y = –4 diperoleh satu nilai x. Sehingga, kedua grafik yang didefinisikan oleh persamaan-persamaan di atas akan berpotongan di tiga titik, yaitu (3, 5), (–3, 5), dan (0, –4). Hasil tersebut dapat didukung oleh grafik dari parabola dan hiperbola dari persamaan-persamaan yang diberikan sebagai berikut.

Dari dua contoh di atas kita telah berlatih untuk menyelesaikan suatu sistem persamaan dari keluarga irisan kerucut. Selesaian tersebut, jika ada, merupakan pasangan-pasangan berurutan yang direpresentasikan sebagai titik-titik potong dari grafik persamaan-persamaan yang diberikan

Contoh Soal Volume Bangun Ruang dan Pembahasan

Tiga buah logam yang berbentuk bola yang memiliki jari-jari 7 cm, dimasukkan ke dalam tabung yang berisi air di dalamnya. Apabila setelah logam tersebut dimasukkan, permukaan air dalam tabung tersebut naik setinggi 2 cm, tentukan jari-jari tabung tersebut!

Pembahasan

Volume tiga bola logam sama dengan volume air yang naik. Sehingga,

Jadi, jari-jari tabung tersebut adalah 7√(14) cm.

Soal dan Pembahasan Simetri Putar

Tentukan tingkat simetri putar yang dimiliki oleh masing-masing bangun datar berikut ini.

Pembahasan

Sekarang mari kita lukis pusat titik pusat dari ketiga bangun datar tersebut.

Bangun datar pertama memiliki tingkat simetri putar 5, yaitu ketika diputar sejauh 72°, 144°, 216 °, 288°, dan 360°. Bangun datar ke-2 memiliki tingkat simetri putar 3, yaitu ketika diputar sejauh 120°, 240°, dan 360°. Sedangkan bangun datar ke-3 memiliki tingkat simetri putar 2, yaitu ketika diputar sejauh 180° dan 360°.

Soal dan Pembahasan Kongruen dan Kesebangunan

Untuk lebih memahami mengenai kesebangunan dan kekongruenan bangun datar, perhatikan beberapa contoh soal berikut.

Contoh 1: Kesebangunan Dua Persegi Panjang

Psersegi panjang ABCD memiliki panjang dan lebar secara berturut-turut 13 cm dan 39 cm. Jika persegi panjang ABCD tersebut sebangun dengan persegi panjang KLMN, yang sisi terpanjangnya memiliki ukuran 24 cm, tentukan panjang sisi terpendek dari persegi panjang KLMN.

Pembahasan Persegi panjang ABCD dan KLMN dapat digambarkan sebagai berikut.

Karena persegi panjang ABCD sebangun dengan KLMN, maka panjang sisi-sisi yang bersesuaian dari kedua persegi panjang tersebut merupakan perbandingan yang senilai. Sehingga,

Jadi, panjang sisi terpendek dari persegi panjang KLMN adalah 8 cm.

Contoh 2: Kesebangunan pada Persegi Panjang

Perhatikan gambar di bawah ini!

Jika diketahui AB = 144 cm dan BC = 108 cm, persegi panjang ABCD, BCGF, dan EHGD merupakan persegi panjang-persegi panjang yang sebangun, tentukan luas daerah AFHE!

Pembahasan Karena persegi panjang ABCD sebangun dengan persegi panjang BCGF, maka

Karena CD = AB = 144 cm dan CG = 81 cm, maka EH = GD = CD – CG = 144 – 81 = 63 cm. Diketahui ABCD juga sebangun dengan EHGD, maka didapatkan

Sehingga, FH = FG – HG = BC – HG = 108 – 47,75 = 60,25 cm. Diperoleh luas dari segi empat AFHE adalah EH × FH = 63 × 60,25 = 3.795,75 cm²

Soal dan Pembahasan Persamaan Linear Satu Variabel

Soal 1: Penjelajah Gua Bawah Tanah

Dua orang penjelajah gua sedang menelusuri dua cabang yang berbeda dari suatu gua bawah tanah. Penjelajah pertama dapat turun 77 meter lebih jauh daripada penjelajah kedua. Jika penjelajah pertama telah turun 433 meter dari permukaan tanah, berapa meterkah panjang cabang gua yang telah dituruni oleh penjelajah kedua?

Pembahasan Misalkan d adalah jarak yang telah ditempuh oleh penjelajah kedua dalam menuruni cabang gua tersebut. Maka permasalahan ini dapat digambarkan sebagai berikut.

Sehingga, dari ilustrasi di atas permasalahan tersebut dapat dimodelkan sebagai persamaan d + 77 = 433.

Jadi, panjang cabang gua yang telah dituruni oleh penjelajah kedua adalah 356 meter dari permukaan tanah