Selamat datang, Kali ini kita akan berbagi tentang Soal dan Pembahasan Sistem Persamaan Linear Tiga Variabel. Silahkan dibaca baik-baik tentang Soal dan Pembahasan Sistem Persamaan Linear Tiga Variabel ini ya.
Penerapan sistem persamaan linear tiga variabel (SPLTV) dapat muncul di berbagai bentuk dan sektor. Di dunia bisnis dan keuangan, SPLTV dapat digunakan untuk mendiversifikasi investasi dan penghitungan pinjaman. Berikut ini contoh penerapan SPLTV dalam keuangan.

Contoh 1: Memodelkan Permasalahan Keuangan
Suatu perusahaan rumahan meminjam Rp 2.250.000.000,00 dari tiga bank yang berbeda untuk memperluas jangkauan bisnisnya. Suku bunga dari ketiga bank tersebut adalah 5%, 6%, dan 7 %. Tentukan berapa pinjaman perusahaan tersebut terhadap masing-masing bank jika bunga tahunan yang harus dibayar perusahaan tersebut adalah Rp 130.000.000,00 dan banyaknya uang yang dipinjam dengan bunga 5% sama dengan dua kali uang yang dipinjam dengan bunga 7%?
Pembahasan Misalkan x, y, dan z secara berturut-turut adalah banyaknya uang yang dipinjam dengan bunga 5%, 6%, dan 7%. Ini berarti yang menjadi persamaan pertama kita adalah x + y + z = 2.250 (dalam jutaan). Persamaan kedua diperoleh dari total bunga pertahunnya, yaitu Rp 130.000.000,00: 0,05x + 0,06y + 0,07z = 130. Sedangkan persamaan ketiga dapat diperoleh dari kalimat, “banyaknya uang yang dipinjam dengan bunga 5% sama dengan dua kali uang yang dipinjam dengan bunga 7%”, sehingga persamaannya adalah x = 2z. Ketiga persamaan tersebut membentuk sistem seperti berikut.

Suku-x pada persamaan pertama adalah 1. Apabila dituliskan kembali ke dalam bentuk standar, sistem tersebut akan menjadi
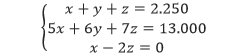
Gunakan –5P1 + P2 untuk mengeliminasi suku-x di P2, dan –P1 + P3 untuk mengeliminasi suku-x di P3.
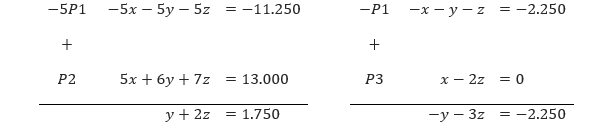
Sehingga, P2 yang baru adalah y + 2z = 1.750 dan P3 yang baru adalah y + 3z = 2.250 (setelah dikalian dengan –1), yang menghasilkan sistem berikut.
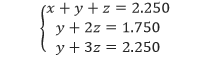
Dengan menyelesaikan subsistem 2 × 2 (dua persamaan terakhir) menggunakan –P2 + P3 menghasilkan z = 500. Selanjutnya dengan menerapkan substitusi balik akan menghasilkan x = 1.000 dan y = 750. Diperoleh selesaian SPLTV tersebut adalah (1.000, 750, 500). Ini berarti bahwa perusahaan tersebut meminjam 1 miliar rupiah pada bunga 5%, 750 juta rupiah pada bunga 6%, dan 500 juta rupiah pada bunga 7%.
No comments:
Post a Comment