Selamat datang, Kali ini kita akan berbagi tentang Penjumlahan dan Pengurangan Matriks. Silahkan dibaca baik-baik tentang Penjumlahan dan Pengurangan Matriks ini ya.
Matriks ternyata punya banyak kegunaan. Salah satunya dalam mencari penyelesaian persamaan linear. Sebelum bisa mengaplikasikan matriks ini, kamu harus tahu terlebih dahulu operasi matematika pad matriks. Dalam kesempatan ini dijelaskan operasi jumlah, operasi kurang dan kesamaan dua matriks.
Agar lebih mudah kamu bisa lihat contoh soal di bawah ini.

Sebuah matriks, dimisalkan matriks A. Anggota atau elemen dari matriks A diberi simbol 'a'. Posisi tersebu dilengkapi dengan indeks yang berfungsi sebagai penunjuk posisinya. Lebih lengkap disimbolkan dengan $a_{ij}$. Dimana i adalah posisi baris dari elemen tersebut dan j adalah posisi kolom pada baris tersebut. Akhirnya sebuah matriks yang utuh bisa ditulis dalam bentuk:
Dalam matriks akan ditemukan istilah Ordo. Ordo artinya adalah ukuarn matriks. Dari contoh matriks di atas artinya memiliki ordo mxn. Artinya matriks A memiliki m baris dan n kolom. Sekarang perhatikan contoh matriks di bawah ini,
 |
| Contoh Matriks |
$A= \begin{pmatrix}1 &4 \\ -2 & 3 \end{pmatrix}$
$B= \begin{pmatrix} 3 & 2\\ 4 &3 \\ -5& 6 \end{pmatrix}$
Matriks A memiliki ordo 2x2. Sementara Matriks B memiliki ordo 3x2. Sekarang bisakah kamu menyebutkan entri $a_{21}$, $b_{12}$.
Untuk $a_{21} =-2$. Kenapa karena posisi baris 2 kolom 1 ditempati oleh angka -2. Begitu juga dengan $b_{12}=2$. Posisi baris 1 kolom dua ditempati oleh angka 2.
Kesamaan Matriks
Untuk mengatakan sama, maka harus ada dua buah yang dibandingkan. Antara dua matriks dikatakan sama bila memiliki ordo yang sama dan nilai setiap entri yang bersesuai juga sama. Misalkan dikatakan matriks A memiliki kesamaan dengan Matriks B. Maka, ordo A = ordo B. Dan setiap entri yang bersesuain
$ a_{11} = b_{11} \\ a_{12} =b_{12} \\ dst.$
Contoh Kesamaan Matriks
$A= \begin{pmatrix} 1 &4 \\ -2 & 3 \end{pmatrix} \\ B=\begin{pmatrix} 3 & -2\\ 1& 4 \end{pmatrix} \\ C=\begin{pmatrix} 3 & -2\\ 1& 4 \end{pmatrix}$
Matriks A tidak sama dengan Matriks B, karena meskipun berordo sama. Entri pada masing masing sama tetapi posisinya berbeda.
Sementara Matriks B memiliki kesamaan dengan matriks C. Karena ordo sama dan entri serta posisi entri nya juga sama.
Operasi Jumlah dan Kurang pada Matriks
Untuk operasi jumlah dan kurang pada matriks harus memenuhi syarat antara ke dua matriks tersebut memiliki ordo yang sama. Jika tidak, maka tidak bisa dilakukan operasi jumlah atau kurang antara ke-dua matriks tersebut. Hasilnya berupa matriks baru dengan ordo yang sama dengan matriks Awal.
Setelah itu baru dilakukan penjumlahan atau pengurangan entri yang seletak.
$a_{11}+b_{11} =... \\ a_{12}+b_{12}=... \\ dst. $

- A + C
- A + B
- C – A
- Karena ordo Matriks A dan matriks C sama, (3 × 2.), maka Matriks A dan C bisa dilakukan operasi jumlah.
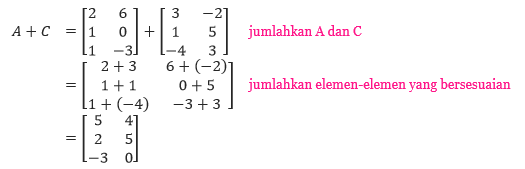
- Karna matriks A dan Matriks B ordonya tak sama, tak bisa dijumlahkan
- Matriks C dan Matriks A memiliki ordo yang sama, maka antara ke dua matriks ini bisa dikurangkan.

Pada pejumlahan Matriks berlaku sifat Komutatif, Asosiatif, identitas dengan ada matriks identitas penjumlahan. Matriks identitas untuk penjumlahan matriks adalah matriks yang semua entrinya adalah 0.