Limit Fungsi

Selamat datang, Kali ini kita akan berbagi tentang Limit Fungsi. Silahkan dibaca baik-baik tentang Limit Fungsi ini ya.

Misalkan kita diminta untuk mensketsa grafik fungsi f, yaitu:

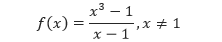
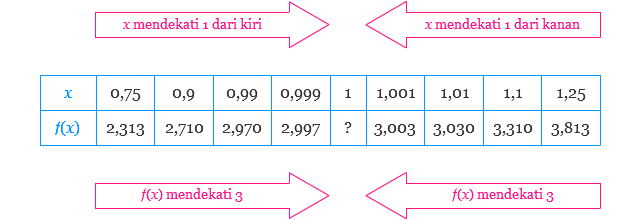
Untuk semua nilai selain x = 1, kita dapat menggunakan teknik-teknik mensketsa kurva seperti biasa. Akan tetapi, ketika x = 1, kita tidak dapat menentukan nilainya. Lalu bagaimana dengan bentuk grafiknya ketika x = 1? Untuk mengetahui sifat grafik fungsi ketika mendekati x = 1, kita dapat menggunakan 2 himpunan nilai x–himpunan xmendekati 1 dari kiri dan himpunan x mendekati 1 dari kanan, seperti yang ditunjukkan oleh tabel berikut.

Grafik dari fungsi f berbentuk parabola yang berlubang pada titik (1, 3), seperti yang ditunjukkan oleh gambar di bawah.

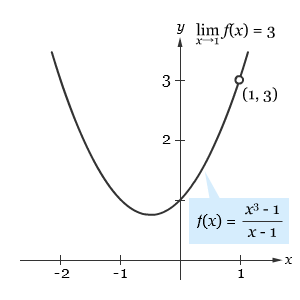
Walaupun x tidak boleh 1, kita dapat menentukan nilai f ketika x mendekati 1 dan diperoleh f(x) akan mendekati 3. Dengan menggunakan notasi limit, kita dapat menulis

Pembahasan ini selanjutnya membawa kita kepada definisi limit yang tidak formal. Jika nilai f(x) mendekati suatu nilai L ketika x mendekati nilai c, maka limit f(x) dengan xmendekati c adalah L. Limit ini dapat ditulis sebagai,

Contoh 1: Menaksir Nilai Limit secara Numerik

Tafsirlah nilai fungsi, f(x) = x/(√(x + 1) – 1) pada beberapa titik yang dekat dengan x = 0 dan gunakan hasil tersebut untuk menentukan nilai limit,

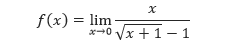
Pembahasan

Tabel berikut menyajikan nilai-nilai f(x) untuk beberapa x yang mendekati 0.

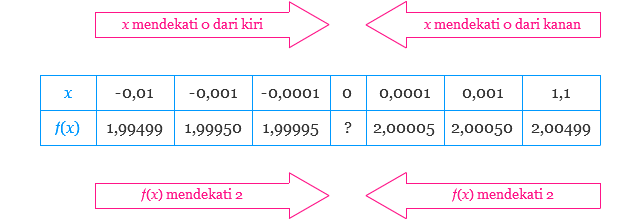
Dari hasil yang ditampilkan tabel, kita dapat menaksirkan nilai limitnya adalah 2. Nilai limit ini diperkuat oleh grafik fungsi f berikut.

Perhatikan bahwa pada contoh 1 di atas, fungsi f tidak terdefinisi di x = 0, namun nilai limit f(x) dapat ditentukan ketika x mendekati 0. Hal ini sering terjadi dan patut dicatat bahwa ada atau tidaknya nilai f(x) pada x = c tidak mempengaruhi keberadaan nilai limit dari f(x) ketika x mendekati c.

Contoh 2: Menemukan Nilai Limit

Tentukan nilai limit dari f(x) ketika x mendekati 2, apabila fungsi f didefinisikan sebagai berikut:

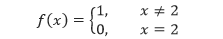
Pembahasan

Karena f(x) = 1 untuk setiap x selain x = 2, maka kita dapat menyimpulkan bahwa nilai limitnya adalah 1, seperti yang ditunjukkan oleh gambar di bawah.

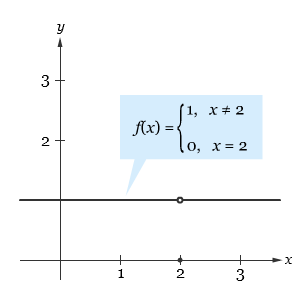
Sehingga kita dapat menuliskan,

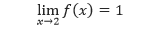
Hal ini sesuai dengan fakta bahwa f(2) = 0 tidak mempengaruhi keberadaan atau nilai limit ketika x mendekati 2. Sebagai contoh, suatu fungsi yang didefinisikan sebagai

Akan memiliki nilai limit yang sama

Semoga postingan kami tentang Limit Fungsi ini bisa bermanfaat dan menambah pengetahuan serta pemahaman matematika kamu. Jangan lupa tetap Berbagi Belajar,Belajar Berbagi.
    dalam: Kelas 11

Share Yuk

   

Postingan Terkait