Selamat datang, Kali ini kita akan berbagi tentang Soal dan Pembahasan Aplikasi Deret Geometri. Silahkan dibaca baik-baik tentang Soal dan Pembahasan Aplikasi Deret Geometri ini ya.
Barisan maupun deret geometri sering digunakan untuk menyelesaikan permasalahan yang sering kita jumpai di sekitar kita. Beberapa permasalahan yang sering menggunakan konsep barisan dan deret geometri adalah permasalahan pada ayunan bandul, depresiasi, penuaan peralatan, laju pertumbuhan populasi, dan lain sebagainya.
Soal 1: Menyelesaikan Penerapan Barisan Geometri: Bandul
Bandul adalah sembarang obyek yang digantungkan pada suatu titik tertentu dan dibiarkan untuk mengayun dengan bebas di bawah pengaruh dari gaya gravitasi. Misalkan ayunan suatu bandul masing-masing panjangnya 0,8 dari ayunan sebelumnya. Lama kelamaan, ayunan bandul tersebut akan semakin pendek dan akan berhenti (walaupun secara teoritis tidak akan pernah berhenti)
- Seberapa panjangkah ayunan ke-6 dari bandul tersebut, apabila panjang ayunan pertamanya adalah 125 cm?
- Berapakah panjang lintasan total yang telah dilalui oleh bandul tersebut sampai ayunan yang ke-6?
- Butuh sampai berapa ayunankah agar panjang dari masing-masing ayunan bandul tersebut kurang dari 14 cm?
- Berapakah panjang lintasan total yang telah dilalui bandul tersebut sampai bandul tersebut berhenti berayun?
Pembahasan Karena panjang masing-masing ayunan sama dengan 0,8 panjang ayunan sebelumnya, maka kita dapat menyimpulkan bahwa panjang ayunan bandul tersebut membentuk barisan geometri.
- Karena panjang ayunan pertamanya adalah 125 cm, maka kita peroleh a1 = 125 dan rasionya r = 0,8. Sehingga beberapa suku pertama dari barisan tersebut adalah 125, 100, 80, dan seterusnya. Untuk suku ke-6, kita dapat menentukannya dengan menggunakan rumus:

Jadi, bandul tersebut mengayun sejauh 40,96 cm pada ayunannya yang ke-6. - Untuk menentukan panjang lintasan total sampai ayunan ke-6, kita hitung S6.

Sehingga, bandul tersebut telah menempuh 461,16 cm sampai ayunan ke-16. - Untuk menentukan banyaknya ayunan ketika masing-masing ayunan panjangnya kurang dari 14 cm, kita selesaikan n pada persamaan 14 = 125(0,8)n – 1.

Jadi, setelah ayunan ke 10 (atau mulai ayunan ke-11), panjang dari lintasan bandul akan kurang dari 14 cm. - Panjang lintasan total sebelum bandul berhenti berayun sama dengan jumlah deret geometri tak hingga dengan a1 = 125 dan r = 0,8.

Sehingga, panjang lintasan yang telah ditempuh oleh bandul sebelum berhenti berayun adalah 625 cm.
Soal 2: Bermain Ayunan
Rhisky sedang bermain ayunan di halaman belakang rumahnya. Dia mengayunkan ayunan tersebut dengan menggunakan tangan dan tubuhnya agar ayunan tersebut berayun sampai ketinggian maksimum, kemudian membiarkannya sampai ayunan yang dia tumpangi berhenti dengan sendirinya. Dalam setiap ayunan, Rhisky menempuh 75% dari panjang ayunan sebelumnya. Jika panjang busur pertama (atau ayunan pertama) 2 meter, tentukan panjang busur yang ditempuh Rhisky pada ayunan ke-8. Berapa meterkah total panjang busur yang ditempuh Rhisky sebelum dia berhenti berayun?
Pembahasan Diketahui panjang busur pertama yang ditempuh Rhisky adalah 2 meter, sehingga kita peroleh a1 = 2. Sedangkan dalam setiap ayunannya dia menempuh 75% dari panjang lintasan sebelumnya. Sehingga r = 75% = 0,75. Untuk menentukan panjang ayunan ke-8, kita tentukan a8 dari barisan tersebut.
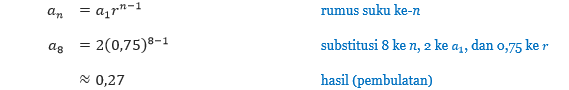
Sehingga, panjang ayunan Rhisky yang ke-8 adalah 0,27 meter atau 27 cm. Selanjutnya kita tentukan panjang lintasan yang ditempuh oleh Rhisky sebelum dia berhenti berayun. Untuk menentukan panjang lintasan ini, kita cari jumlah deret tak hingga dari barisan tersebut.

Jadi panjang lintasan yang telah ditempuh oleh Rhisky sampai dia berhenti berayun adalah 8 meter.
Soal 3: Permasalahan Depresiasi
Suatu mobil SUV baru mengalami depresiasi nilai jual sebesar 15% tiap tahunnya (hal ini berarti harga jualnya menjadi 85% dari harga jual tahun sebelumnya). Jika harga beli dari mobil SUV baru tersebut adalah 510 juta rupiah, berapakah harga jual dari SUV tersebut setelah 5 tahun? Berapa tahunkah sampai harga SUV tersebut kurang dari 100 juta rupiah?
Pembahasan Harga jual suatu SUV sama dengan 85% dari harga tahun sebelumnya, sehingga kita peroleh r = 85% = 0,85. Harga beli mobil SUV baru tersebut adalah 510 juta rupiah, atau dengan kata lain a0 = 510 (dalam juta). Akibatnya, harga jual pada tahun pertama a1 = 510 ∙ 0,85 = 433,5. Sehingga dalam menentukan harga jual SUV tersebut setelah 5 tahun, kita akan tentukan a5.
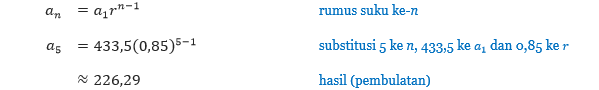
Kita peroleh bahwa harga jual SUV tersebut setelah 5 tahun adalah 226,29 juta rupiah. Selanjutnya kita tentukan sampai tahun ke berapa ketika harga SUV tersebut kurang dari 100 juta rupiah. Permasalahan tersebut dapat diselesaikan dengan menentukan nilai ndari persamaan

Jadi, setelah tahun ke-10 (atau mulai tahun ke-11) harga SUV tersebut akan kurang dari 100 juta rupiah.
No comments:
Post a Comment