Selamat datang, Kali ini kita akan berbagi tentang Penyelesaian Integral Subtitusi Trigonometri. Silahkan dibaca baik-baik tentang Penyelesaian Integral Subtitusi Trigonometri ini ya.
Substitusi trigonometri dapat digunakan untuk menyelesaikan integral yang memuat bentuk akar

Tujuan dari penggunaan substitusi trigonometri adalah untuk menghilangkan akar tersebut dalam integran. Kita dapat melakukan hal ini dengan menggunakan identitas Pythagoras
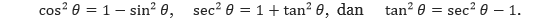
Sebagai contoh, jika a > 0, misalkan u = a sin θ, dengan –π/2 < θ < π/2. Maka

Perhatikan bahwa cos θ ≥ 0, karena –π/2 < θ < π/2.
Substitusi Trigonometri
- Untuk integral yang memuat √(a² – u²), misalkan u = a sin θ. Maka, didapatkan √(a² – u²) = a cos θ, di mana –π/2 < θ < π/2.

- Untuk integral yang memuat √(a² + u²), misalkan u = a tan θ.
Maka, √(a² + u²) = a sec θ, dengan –π/2 < θ < π/2.
- Untuk integral yang memuat √(u² – a²), misalkan u = a sec θ. Maka,


Catatan Batasan dari θ memastikan bahwa fungsi pada substitusi tersebut merupakan fungsi satu-satu. Faktanya, batasan tersebut merupakan interval yang sama di mana arcsinus, arctangen, dan arcsecan didefinisikan.
No comments:
Post a Comment