Selamat datang, Kali ini kita akan berbagi tentang Penyelesaian SPLDV dengan Metode Eliminasi. Silahkan dibaca baik-baik tentang Penyelesaian SPLDV dengan Metode Eliminasi ini ya.
sistem persamaan linear dua variabel (SPLDV) juga dapat diselesaikan dengan menggunakan metode eliminasi. Dengan menggunakan metode ini, kita harus mengeliminasi/menghilangkan salah satu variabel dengan cara penjumlahan ataupun pengurangan. Untuk lebih jelasnya perhatikan contoh berikut.
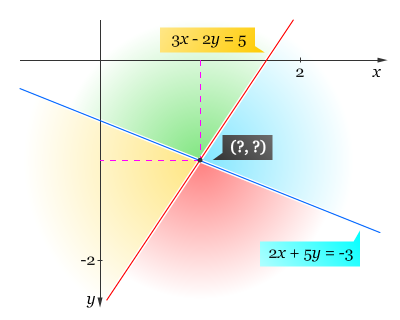
Tentukan himpunan selesaian dari SPLDV yang memuat persamaan-persamaan 2x + 5y = –3 dan 3x – 2y = 5.
Grafik dari kedua persamaan tersebut dapat digambarkan sebagai berikut.
Untuk menentukan selesaiannya, pertama kita harus mengeliminasi salah satu variabelnya. Misalkan kita akan mengeliminasi variabel x, maka kita harus menyamakan koefisien x dari kedua persamaan tersebut. Koefisien x pada persamaan 1 dan 2 secara berturut-turut adalah 2 dan 3. Sehingga kita harus menyamakan koefisien x dari kedua persamaan tersebut menjadi KPK dari 2 dan 3, yaitu 6, dengan mengalikan persamaan 1 dengan 3 dan persamaan 2 dengan 2.
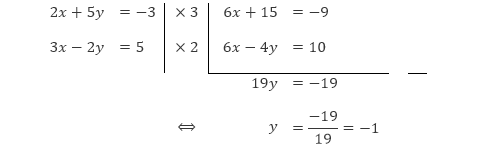
Dengan cara yang sama, kita dapat mengeliminasi variabel y untuk mendapatkan nilai dari x.
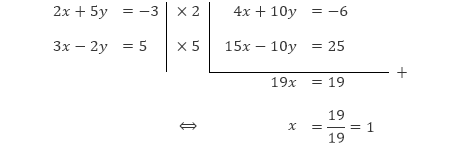
Sehingga diperoleh selesaiannya adalah x = 1 dan y = –1, atau dapat dituliskan sebagai himpunan selesaian Hp = {(1, –1)}.
Menyelesaikan SPLDV dengan Menggunakan Metode Campuran
Metode eliminasi juga dapat dipadukan dengan metode substitusi dalam menyelesaikan suatu permasalahan SPLDV. Perhatikan contoh berikut.
Selisih umur seorang ayah dan anak perempuannya adalah 26 tahun, sedangkan lima tahun yang lalu jumlah umur keduanya 34 tahun. Hitunglah umur ayah dan anak perempuannya dua tahun yang akan datang.
Misalkan umur ayah dan anak perempuannya secara berturut-turut adalah m dan n, maka permasalahan di atas dapat dimodelkan sebagai berikut.
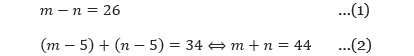
Grafik dari persamaan-persamaan m – n = 26 dan m + n = 44 dapat digambarkan seperti berikut.
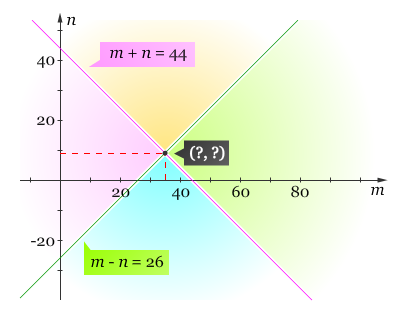
Pertama, kita akan mengeliminasi variabel n untuk mendapatkan nilai dari m dengan menjumlahkan persamaan 1 dengan persamaan 2.
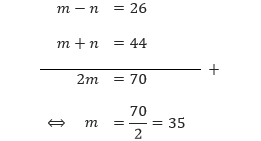
Selanjutnya kita substitusikan m = 35 ke salah satu persamaan, misalkan ke persamaan 1. Sehingga diperoleh,
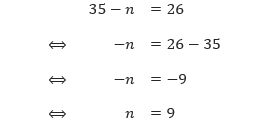
Jadi, umur ayah dan anak perempuannya saat ini secara berturut-turut adalah 35 tahun dan 9 tahun.
No comments:
Post a Comment