Selamat datang, Kali ini kita akan berbagi tentang Cara menyelesaikan Pertidaksamaan Nilai Mutlak. Silahkan dibaca baik-baik tentang Cara menyelesaikan Pertidaksamaan Nilai Mutlak ini ya.
A. Kurang Dari/ Kecil dari
nilai mutlak dapat diselesaikan dengan menggunakan konsep dasar dari sifat persamaan nilai mutlak. Persamaan |x| = 5 meminta kita untuk menentukan semua bilangan x yang memiliki jarak 5 dengan titik 0, sedangkan pertidaksamaan |x| < 5 meminta kita untuk menentukan semua bilangan x yang memiliki jarak kurang dari 5 dengan titik 0.
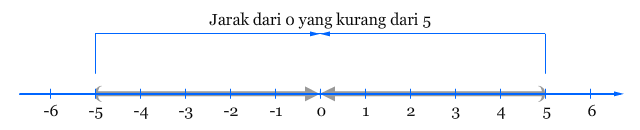
Seperti ilustrasi dari gambar di atas, selesaian dari pertidaksamaan |x| < 5 adalah x > –5 dan x < 5, yang juga dapat dituliskan ke dalam pertidaksamaan gabungan –5 < x < 5. Ilustrasi ini dapat digunakan untuk membangun konsep sifat pertidaksamaan nilai mutlak berikut.
Sifat I: Pertidaksamaan Nilai Mutlak
Jika X adalah suatu bentuk aljabar dan k adalah bilangan real positif, maka |X| < k akan mengimplikasikan –k < X < k.
Contoh: Pertidaksamaan Nilai Mutlak “Kurang Dari”
Tentukan himpunan selesaian dari pertidaksamaan-pertidaksamaan: |3x + 2|/4 ≤ 1 dan |2x – 7| < –5.
Pembahasan Untuk menyelesaikan pertidaksamaan |3x + 2|/4 ≤ 1, kita harus mengisolasi simbol nilai mutlak di satu ruas.
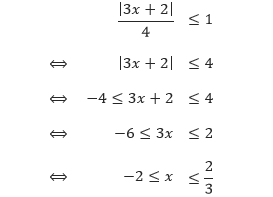
Sehingga, himpunan selesaian dari pertidaksamaan |3x + 2|/4 ≤ 1 adalah { x | –2 ≤ x ≤ 2/3, x bilangan real}. Selanjutnya, perhatikan pertidaksamaan |2x – 7| < –5. Karena nilai mutlak dari setiap bilangan adalah positif atau nol, maka himpunan selesaian dari pertidaksamaan tersebut adalah himpunan kosong, Ø.
B. Lebih Dari/Besar Dari
Untuk pertidaksamaan nilai mutlak “lebih dari”, perhatikan |x| > 2. Sekarang, kita diminta untuk menentukan semua bilangan yang memiliki jarak lebih dari 2 dengan titik 0. Seperti yang ditunjukkan oleh gambar di bawah, selesaiannya adalah semua bilangan dalam interval sebelah kiri dari –2, atau di sebelah kanan 2. Interval-interval tersebut saling disjoin dan simetris terhadap titik 0. Sehingga, selesaian dari |x| > 2 dapat dituliskan sebagai x < –2 atau x > 2.
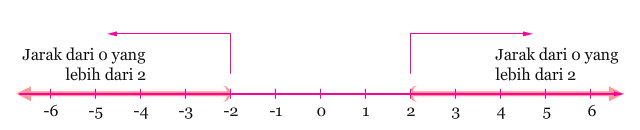
Ilustrasi di atas, dapat digunakan untuk membangun konsep mengenai sifat pertidaksamaan nilai mutlak berikut.
Sifat II: Pertidaksamaan Nilai Mutlak
Jika X adalah suatu bentuk aljabar dan k adalah bilangan real positif, maka |X| > k akan mengimplikasikan bahwa X < –k atau X > k.
Contoh: Menyelesaikan Pertidaksamaan Nilai Mutlak “Lebih Dari”
Tentukan himpunan selesaian dari pertidaksamaan-pertidaksamaan: –1/3 |3 + x/2| < –2 dan |5x + 2| ≥ 3/2.
Pembahasan Perhatikan bahwa –1/3 |3 + x/2| < –2 merupakan pertidaksamaan kurang dari. Tetapi jika kita mengalikan kedua ruas dengan –3, kita harus membalik tanda pertidaksamaannya menjadi lebih dari.
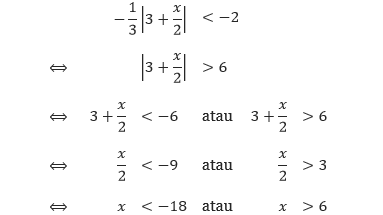
Sehingga himpunan selesaian dari pertidaksamaan tersebut adalah { x | x < –18 atau x > 6, x bilangan real}. Karena nilai mutlak dari semua bilangan adalah positif maka selesaian dari |5x + 2| ≥ 3/2 adalah semua bilangan real. Sehingga himpunan selesaiannya adalah himpunan bilangan real.
No comments:
Post a Comment