Langkah Melukis Garis Singgung Persekutuan Luar Lingkaran

Sebelum kita melukis garis singgung persekutuan dua lingkaran, sebaiknya kita ketahui terlebih dulu pengertian garis singgung persekutan dua lingkaran. Garis singgung persekutuan dua lingkaran adalah garis yang menyinggung kedua lingkaran. Perhatikan gambar di bawah ini:

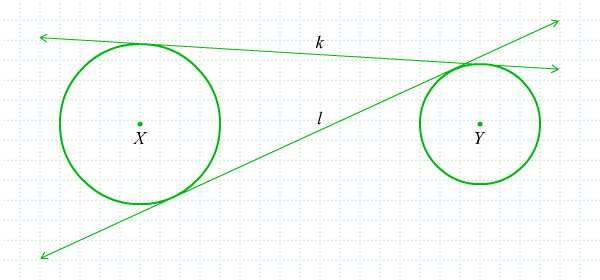
Garis k dan garis l di atas merupakan garis singgung persekutuan lingkaran X dan lingkaran Y. Terdapat dua jenis garis singgung persekutuan dua lingkaran, yaitu garis singgung persekutuan dalam dan garis singgung persekutuan luar. Garis k pada gambar di atas disebut garis singgung persekutuan luar, sedangkan garis l disebut garis singgung persekutuan dalam lingkaran X dan lingkaran Y. Pada pembahasan ini hanya akan dibahas topik melukis garis singgung persekutuan luar dua lingkaran.

Melukis Garis Singgung Persekutuan Luar Dua Lingkaran

Untuk melukis garis singgung persekutuan luar dari dua lingkaran dapat dilakukan dengan langkah-langkah sebagai berikut:

1. Lukislah dua lingkaran yang masing-masing berpusat di titik A dan titik B dengan jari-jari r1 dan r2 kemudian hubungkan kedua titik pusat tersebut.
2. Lukis busur lingkaran dengan pusat di titik A dan B sehingga berpotongan di titik-titikC dan D. Kemudian hubungkan titik-titik C dan D tersebut sehingga memotong ruas garis AB di titik E.
3. Lukislah lingkaran dengan pusat di titik E dengan jari-jari EA.
4. Lukislah lingkaran dengan pusat di titik A dengan panjang jari-jari r1 – r2 sedemikian sehingga memotong lingkaran yang berpusat di titik E di titik-titik X dan Y, kemudian hubungkan titik A dengan titik X dan titik A dengan titik Y sehingga memotong lingkaran A di titik-titik F dan G.
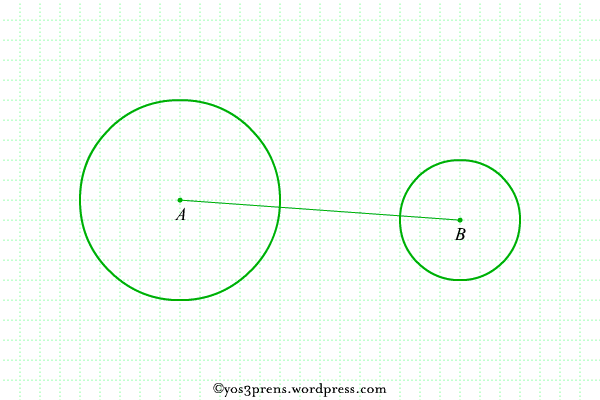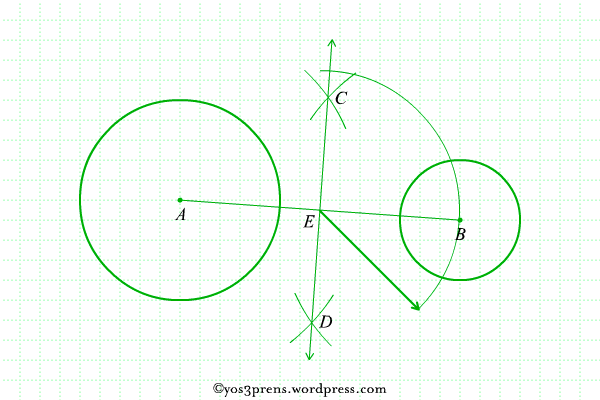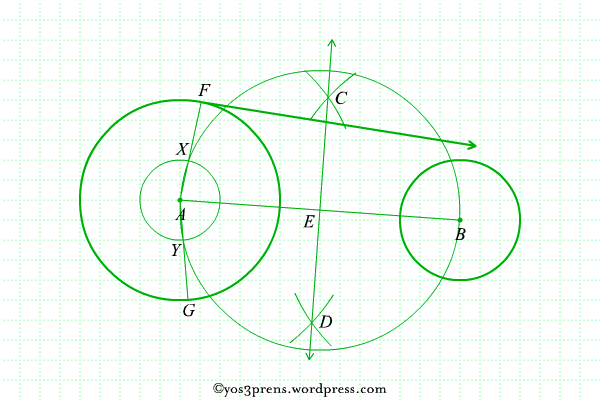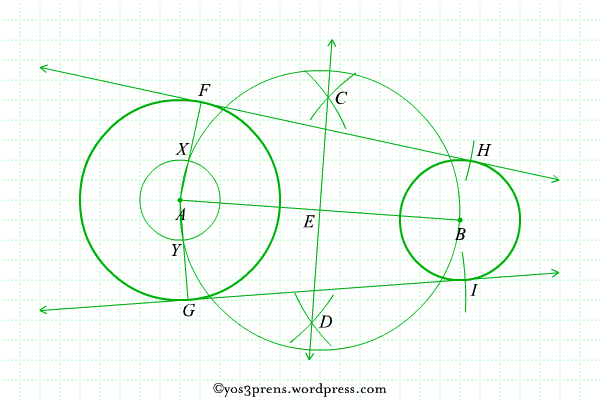
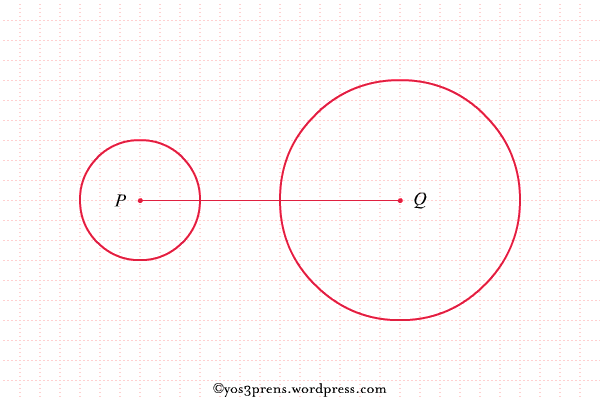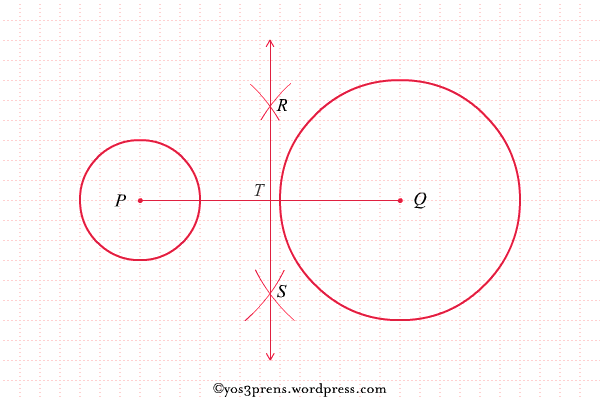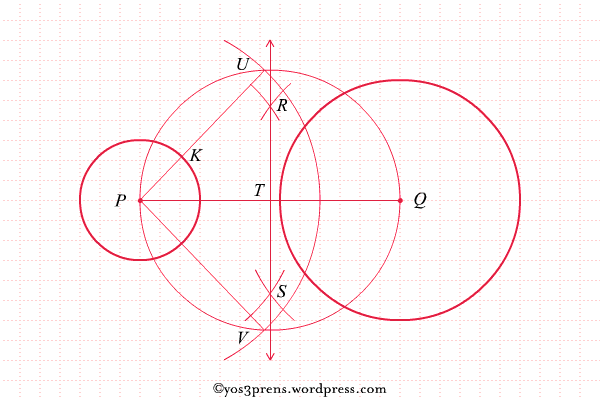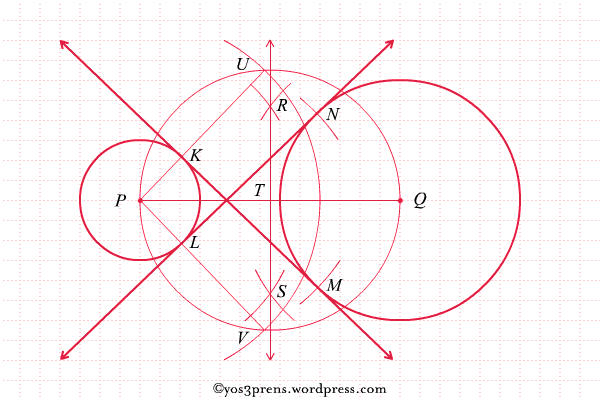
5. Lukislah lingkaran yang berpusat di titik F dengan jari-jari XB sehingga memotong lingkaran B di titik H, kemudian lukis juga lingkaran dengan pusat di titik G dengan hari-jari YB sehingga memotong lingkaran B di titik I.
6. Hubungkan titik F dengan titik H dan titik G dengan titik I sehingga terbentuk garisFH dan garis GI. Garis-garis FH dan GI yang terbentuk merupakan garis singgung persekutuan luar dari lingkaran A dan lingkaran B.

Langkah nomor 1 sampai dengan 6 dalam melukis garis singgung persekutuan luar dari lingkaran A dan lingkaran B tersebut dapat diilustrasikan sebagai berikut:

Langkah Melukis Garis Singgung Persekutuan dalam Lingkaran

Melukis garis singgung persekutuan dalam dari dua lingkaran dapat dilakukan dengan langkah-langkah seperti berikut ini:

1. Lukislah dua lingkaran yang masing-masing berpusat di titik P dan titik Q dengan jari-jari r1 dan r2 kemudian hubungkan kedua titik pusat tersebut.
2. Lukislah busur lingkaran dengan pusat di titik P dan Q sehingga berpotongan di titik-titik R dan S. Kemudian hubungkan titik RS sehingga memotong PQ di titik T.
3. Lukislah lingkaran dengan pusat di titik T dengan jari-jari TP.
4. Lukislah lingkaran dengan pusat di titik P yang panjang jari-jarinya r1 + r2 sedemikian sehingga memotong lingkaran yang berpusat di titik T di titik-titik U dan V, kemudian hubungkan titik P dengan U dan V, sehingga memotong lingkaran P di titik-titik K danL.
5. Lukislah busur lingkaran dengan pusat di titik K dengan panjang jari-jarinya sama dengan UQ sedemikian sehingga memotong lingkaran Q pada titik M, kemudian lukis juga busur lingkaran dengan pusat L dengan panjang jari-jarinya sama dengan VQsedemikian sehingga memotong lingkaran Q pada titik N.
6. Hubungkan titik K dengan titik M dan titik L dengan titik N. Garis-garis KM dan LNmerupakan garis singgung persekutuan dalam lingkaran P dan lingkaran Q.

Langkah 1 sampai dengan 6 dalam melukis garis singgung persekutuan dalam lingkaran di atas dapat diilustrasikan sebagai berikut.

Langkah Menggambar Diagram Batang

Dalam suatu sekolah, terdapat 5 kelas untuk kelas IX, yaitu kelas IX A sampai IX E. Pada suatu ujian matematika, masing-masing kelas IX tersebut memiliki nilai rata-rata berikut: Kelas IX A memiliki rata-rata 77,5, rata-rata kelas IX B 79,2, rata-rata kelas IX C 85,8, rata-rata kelas IX D 76,7, dan rata-rata kelas IX E 84,3. Nilai rata-rata tersebut akan sedikit sulit untuk dibandingkan apabila disajikan dalam bentuk kalimat seperti sebelumnya. Terdapat cara menyajikan data yang dapat memudahkan kita untuk memudahkan dalam membandingkan masing-masing kategori, yaitu dengan diagram batang.

Langkah pertama dalam membuat diagram batang adalah membuat dua sumbu mendatar dan tegak. Sumbu mendatar memperlihatkan kategori, sedangkan sumbu tegak menyatakan nilai/frekuensi dari masing-masing kategori. Berikut ini contoh diagram batang yang menyajikan data rata-rata nilai ujian matematika kelas IX A – IX E pada kasus sebelumnya.

Dari diagram batang di atas kita dapat mengamati bahwa kelas IX A, IX B, dan IX D merupakan kelas yang memiliki rata-rata yang hampir sama dan berada di bawah dua kelas lainnya, yaitu kelas IX C dan IX E.

Selanjutnya perhatikan tabel yang menyajikan data suhu terendah dan tertinggi dari beberapa kota berikut!

Dari tabel tersebut kita dapat menggambar diagram batang yang menyajikan suhu terendah dan tertinggi dari masing-masing kota sekaligus. Perhatikan diagram batang berikut!

Dari dua diagram batang pada contoh sebelumnya, kita dapat membandingkan nilai dari masing-masing kategori. Pada diagram pertama, kita dapat membandingkan nilai rata-rata dari masing-masing kelas IX. Sedangkan pada diagram kedua, kita dapat membandingkan suhu terendah dan suhu tertinggi sekaligus dari masing-masing kota. Dari kedua contoh tersebut kita dapat menyimpulkan bahwa diagram batang sangat tepat digunakan untuk membandingkan nilai/frekuensi dari masing-masing kategori.

Penurunan Rumus Volume Limas dan Kerucut

Menemukan Rumus Volume Limas dan Kerucut

Dalam melakukan investigasi ini, kalian akan menggunakan sepasang wadah yang berbentuk prisma dan limas, sepasang wadah yang berbentuk tabung dan kerucut, serta air. Siapkan benda-benda tersebut, kemudian lakukan langkah-langkah berikut:

1. Pilihlah prisma dan limas yang memiliki alas dan tinggi yang kongruen.
2. Isilah limas tersebut dengan air hingga penuh, kemudian tuangkan air tersebut ke dalam prisma hingga tanpa sisa. Berapa bagiankah air tersebut mengisi prisma tersebut?
3. Cek jawabanmu dengan mengulangi langkah ke-2 hingga prisma penuh terisi air.

Pilihlah tabung dan kerucut yang memiliki alas dan tinggi yang kongruen kemudian ulangi langkah ke-2 dan ke-3.

Apa yang dapat kamu simpulkan dari investigasi di atas? Bagaimana hubungkan antara volume prisma dengan limas, dan volume tabung dengan volume kerucut? Setelah kita lakukan investigasi di atas, ternyata kita temukan bahwa volume prisma sama dengan tiga kali volume limas. Atau dengan kata lain volume limas sama dengan sepertiga dari volume prisma. Hubungan ini juga berlaku untuk kerucut dan tabung. Karena rumus volume prisma dan tabung adalah V = A ∙ t, untuk A luas alas dan t tinggi prisma atau tabung, maka volume dari limas dan kerucut dapat dirumuskan sebagai berikut.

Rumus Volume Limas dan KerucutJika A dan t secara berturut-turut adalah luas alas dan tinggi dari limas atau kerucut, maka volume dari limas atau kerucut tersebut adalah V = 1/3 ∙ A ∙ t.

Sehingga, untuk mencari volume dari limas atau kerucut, pertama-tama kita harus menentukan luas dari alasnya. Setelah itu kalikan luas alas tersebut dengan sepertiga dan tinggi dari limas atau kerucut tersebut. Untuk lebih memahami mengenai volume limas dan kerucut, perhatikan contoh soal berikut.

Contoh Soal

Tentukanlah volume dari masing-masing bangun ruang berikut. Semua satuan ukuran yang digunakan adalah cm.

Gambar (i) adalah kerucut, gambar (ii) adalah limas persegi, sedangkan gambar (iii) adalah tabung yang dipotong oleh kerucut.

Pembahasan Contoh Soal

Volume dari kerucut yang memiliki jari-jari alas 9 cm dan tinggi 16 cm dapat ditentukan sebagai berikut.

V = 1/3 ∙ A ∙ t = 1/3 ∙ π ∙ r2 ∙ t = 1/3 ∙ π ∙ 92 ∙ 16 = 432π

Sehingga, volume dari kerucut di atas adalah 432π cm2. Volume dari limas persegi yang memiliki sisi alas 8 cm dan tingginya 21 cm dapat dicari sebagai berikut.

V = 1/3 ∙ A ∙ t = 1/3 ∙ 82 ∙ 21 = 448

Sehingga, volume dari limas persegi tersebut adalah 448 cm2. Sedangkan volume tabung yang dipotong oleh kerucut dengan diameter 18 cm dan tinggi 35 cm dapat dicari seperti berikut.

V = A ∙ t – 1/3 ∙ A ∙ t = 2/3 ∙ A ∙ t = 2/3 ∙ (1/4 ∙ π ∙ d2) ∙ t = 2/3 ∙ (1/4 ∙ π ∙ 182) ∙ 35 = 1.890π

Jadi, volume dari tabung yang dipotong oleh kerucut di atas adalah 1.890π cm2

Penyelesaian Integral Subtitusi Trigonometri

Substitusi trigonometri dapat digunakan untuk menyelesaikan integral yang memuat bentuk akar

Tujuan dari penggunaan substitusi trigonometri adalah untuk menghilangkan akar tersebut dalam integran. Kita dapat melakukan hal ini dengan menggunakan identitas Pythagoras

Sebagai contoh, jika a > 0, misalkan u = a sin θ, dengan –π/2 < θ < π/2. Maka

Perhatikan bahwa cos θ ≥ 0, karena –π/2 < θ < π/2.

Substitusi Trigonometri

1. Untuk integral yang memuat √(a² – u²), misalkan u = a sin θ. Maka, didapatkan √(a² – u²) = a cos θ, di mana –π/2 < θ < π/2.
   
2. Untuk integral yang memuat √(a² + u²), misalkan u = a tan θ.
   Maka, √(a² + u²) = a sec θ, dengan –π/2 < θ < π/2.
   
3. Untuk integral yang memuat √(u² – a²), misalkan u = a sec θ. Maka,
   
   

Catatan Batasan dari θ memastikan bahwa fungsi pada substitusi tersebut merupakan fungsi satu-satu. Faktanya, batasan tersebut merupakan interval yang sama di mana arcsinus, arctangen, dan arcsecan didefinisikan.

Cara Menentukan Nilai Optimum Program Linear dengan Metode Garis Selidik

Untuk menentukan nilai optimum fungsi objektif dengan menggunakan metode garis selidik, lakukanlah langkah-langkah berikut:

1. Tentukan model pertidaksamaan dari informasi soal dan gambarkan daerah selesaian dari sistem pertidaksamaan tersebut pada bidang koordinat.
2. Tentukan garis selidik ax + by = k apabila fungsi objektifnya f(x, y) = ax + by, a, b, dank bilangan real.
3. Untuk menentukan nilai maksimum fungsi objektif maka carilah garis selidik dengan nilai k terbesar dan melalui titik (-titik) pada daerah selesaian. Sedangkan untuk menentukan nilai minimum fungsi objektif maka carilah garis selidik dengan nilai k terkecil dan melalui titik (-titik) pada daerah selesaian.

Untuk lebih memahami penerapan langkah-langkah tersebut, perhatikan contoh soal berikut.

Contoh Soal

Seorang peternak ayam petelur harus memberi makanan untuk tiap 50 ekor/hari paling sedikit 150 unit zat A dan 200 unit zat B. Zat-zat tersebut tidak dapat dibeli dalam bentuk murni, melainkan teerdapat dalam makanan ayam M1 dan M2. Tiap kg makanan ayam M1 mengandung 30 unit zat A dan 20 unit zat B, dan makanan M2 mengandung 20 unit zat A dan 40 unit zat B. Jika harga M1 adalah Rp 225/kg dan harga M2 adalah Rp 250/kg, dan tiap ekor membutuhkan 125 gr makanan/hari. Berapakah banyaknya makanan M1 dan M2 harus dibeli tiap hari untuk 1000 ekor ayam petelur, supaya harganya semurah-murahnya dan kebutuhan akan zat-zat itu dipenuhi?

Pembahasan Contoh Soal

Langkah pertama: Ubah permasalahan di atas menjadi model matematika. Misalkan xdan y secara berturut adalah banyaknya makanan M1 dan M2 yang harus dibeli tiap hari untuk 1000 ekor ayam petelur. Karena tiap 50 ekor ayam dalam tiap harinya harus makan paling sedikit 150 unit zat A dan 200 unit zat B, tiap 1.000 ekor ayam dalam tiap harinya harus makan paling sedikit 3.000 unit zat A dan 4.000 unit zat B maka. Dan karena tiap ekor membutuhkan 125 gr makanan/hari, maka 1.000 ekor ayam membutuhkan 125.000 gr atau 125 kg makanan tiap harinya. Sehingga permasalahan di atas dapat dimodelkan sebagai berikut.

30x + 20y ≥ 3.000
20x + 40y ≥ 4.000
x + y ≥ 125
x ≥ 0
y≥ 0
x, y bilangan cacah

Fungsi objektif dari permasalahan di atas adalah f(x, y) = 225x + 250y. Sebelum menggambar grafiknya, sebaiknya kita daftar titik-titik yang dilalui oleh garis-garis batas dari sistem pertidaksamaan di atas.

Apabila digambarkan, daerah selesaiannya seperti berikut.

Langkah kedua: Gambarkan garis selidik 225x + 250y = k.

Setelah melihat gambar di atas, ternyata garis selidik yang melalui titik (50, 75) yang memiliki nilai k minimum (nilai k bisa dilihat pada sumbu y, semakin tinggi titik potong garis selidik terhadap sumbu y, maka semakin besar pula nilai k tersebut, dan sebaliknya). Untuk x = 50 dan y = 75, diperoleh nilai k-nya adalah 30.000.

Jadi, banyaknya makanan M1 dan M2 harus dibeli tiap hari untuk 1000 ekor ayam petelur supaya harganya semurah-murahnya dan kebutuhan akan zat-zat itu dipenuhi secara berturut-turut adalah 50 kg dan 75 kg.

Baca Juga : Cara Menentukan Nilai Optimum Program Linear dengan Metode Titik Pojok

Relasi Rekursif Homogen Linear Berderajat Dua dengan Koefisien Konstanta

Metode ini merupakan teknik dasar yang tidak membutuhkan teknik khusus kecuali kemampuan untuk menemukan pola. Akan tetapi, pada banyak kasus, pola pada barisan tertentu tidak dapat dilihat secara jelas sehingga kita membutuhkan metode lain dalam menentukan rumus eksplisit tersebut. Terdapat berbagai macam metode yang dapat digunakan untuk menentukan rumus eksplisit dari barisan yang didefinisikan secara rekursif. Metode yang dijelaskan pada pembahasan ini merupakan salah satu metode yang dapat digunakan untuk menentukan rumus eksplisit dari barisan Fibonacci dan barisan-barisan sejenis lainnya.

Definisi
Relasi rekursif homogen linear berderajat dua dengan koefisien konstanta merupakan relasi rekursif yang memiliki bentuk,

untuk setiap bilangan bulat k ≥ bilangan bulat tertentu, di mana A dan B merupakan suatu konstanta bilangan real, dengan B ≠ 0.

Relasi rekursif tersebut dikatakan “berderajat dua” karena ak dinyatakan dalam dua suku sebelumnya, ak – 1 dan ak – 2, dikatakan “linear” karena ak – 1 dan ak – 2 muncul pada suku yang berbeda dan masing-masing memiliki pangkat satu, dikatakan “homogen” karena total derajat dari masing-masing sukunya sama (sehingga tidak ada suku konstanta), dan “koefisien konstanta” karena A dan B merupakan suatu konstanta yang tidak bergantung terhadap k.

Contoh 1: Relasi Rekursif Homogen Linear Berderajat Dua dengan Koefisien Konstanta

Nyatakan apakah masing-masing relasi rekursif berikut merupakan relasi rekursif homogen linear berderajat dua dengan koefisien konstanta atau bukan:

1. ak = (–4)ak – 1 + (k + 1)ak – 2
2. bk = bk – 1 + bk – 2
3. ck = (ck – 1)2 + ck – 1 ∙ ck – 2
4. dk = dk – 1 + dk – 2 + dk – 3
5. ek = 2ek – 2
6. fk = 2fk – 1 + 3fk – 2 – 5

Pembahasan Kita dapat mengidentifikasi relasi-relasi rekursif tersebut dengan menggunakan definisi di atas.

1. Bukan; koefisiennya bukan konstanta.
2. Iya; A = 1 = B.
3. Bukan; tidak linear.
4. Bukan; tidak berderajat dua.
5. Iya; A = 0 dan B = 2.
6. Bukan; tidak homogen.