Selamat datang, Kali ini kita akan berbagi tentang Relasi Rekursif Homogen Linear Berderajat Dua dengan Koefisien Konstanta. Silahkan dibaca baik-baik tentang Relasi Rekursif Homogen Linear Berderajat Dua dengan Koefisien Konstanta ini ya.
Metode ini merupakan teknik dasar yang tidak membutuhkan teknik khusus kecuali kemampuan untuk menemukan pola. Akan tetapi, pada banyak kasus, pola pada barisan tertentu tidak dapat dilihat secara jelas sehingga kita membutuhkan metode lain dalam menentukan rumus eksplisit tersebut. Terdapat berbagai macam metode yang dapat digunakan untuk menentukan rumus eksplisit dari barisan yang didefinisikan secara rekursif. Metode yang dijelaskan pada pembahasan ini merupakan salah satu metode yang dapat digunakan untuk menentukan rumus eksplisit dari barisan Fibonacci dan barisan-barisan sejenis lainnya.
Definisi
Relasi rekursif homogen linear berderajat dua dengan koefisien konstanta merupakan relasi rekursif yang memiliki bentuk,
untuk setiap bilangan bulat k ≥ bilangan bulat tertentu, di mana A dan B merupakan suatu konstanta bilangan real, dengan B ≠ 0.
Relasi rekursif tersebut dikatakan “berderajat dua” karena ak dinyatakan dalam dua suku sebelumnya, ak – 1 dan ak – 2, dikatakan “linear” karena ak – 1 dan ak – 2 muncul pada suku yang berbeda dan masing-masing memiliki pangkat satu, dikatakan “homogen” karena total derajat dari masing-masing sukunya sama (sehingga tidak ada suku konstanta), dan “koefisien konstanta” karena A dan B merupakan suatu konstanta yang tidak bergantung terhadap k.

Contoh 1: Relasi Rekursif Homogen Linear Berderajat Dua dengan Koefisien Konstanta
Nyatakan apakah masing-masing relasi rekursif berikut merupakan relasi rekursif homogen linear berderajat dua dengan koefisien konstanta atau bukan:
- ak = (–4)ak – 1 + (k + 1)ak – 2
- bk = bk – 1 + bk – 2
- ck = (ck – 1)2 + ck – 1 ∙ ck – 2
- dk = dk – 1 + dk – 2 + dk – 3
- ek = 2ek – 2
- fk = 2fk – 1 + 3fk – 2 – 5
Pembahasan Kita dapat mengidentifikasi relasi-relasi rekursif tersebut dengan menggunakan definisi di atas.
- Bukan; koefisiennya bukan konstanta.
- Iya; A = 1 = B.
- Bukan; tidak linear.
- Bukan; tidak berderajat dua.
- Iya; A = 0 dan B = 2.
- Bukan; tidak homogen.
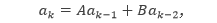
No comments:
Post a Comment