Selamat datang, Kali ini kita akan berbagi tentang Menghitung Jumlah Deret Geometri. Silahkan dibaca baik-baik tentang Menghitung Jumlah Deret Geometri ini ya.
Jumlah dari n suku pertama suatu barisan geometri disebut sebagai deret geometri. Jika suku ke-n dari barisan geometri dirumuskan: an = a1rn – 1, maka deret geometri dapat dituliskan sebagai,
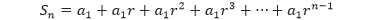
Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita mendapatkan
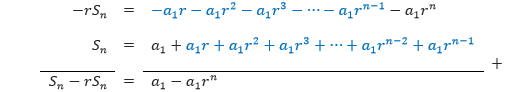
Sehingga kita memperoleh Sn – rSn = a1 – a1rn. Dengan menyelesaikan persamaan tersebut untuk Sn, kita mendapatkan

Hasil di atas merupakan rumus jumlah n suku pertama dari barisan geometri.
Jumlah n Suku Pertama Barisan Geometri
Diberikan suatu barisan geometri dengan suku pertama a1 dan rasio r, jumlah n suku pertamanya adalah
Atau bisa dikatakan: Jumlah dari barisan geometri sama dengan selisih dari suku pertama dan suku n + 1, kemudian dibagi dengan 1 dikurangi rasionya.
Contoh 1: Menghitung Deret Geometri
Hitunglah jumlah 9 suku pertama dari barisan an = 3n.
Pembahasan Jumlah 9 suku pertama dapat juga dinotasikan ke dalam notasi sigma sebagai berikut.

Dari deret tersebut kita dapat memperoleh suku pertama a1 = 3, rasio r = 3, dan banyaknya suku n = 9. Dengan menggunakan rumus jumlah n suku pertama, kita mendapatkan

Jadi, jumlah sembilan suku pertama dari barisan an = 3n adalah 29.523.

No comments:
Post a Comment