Selamat datang, Kali ini kita akan berbagi tentang Langkah Mudah Perkalian Matriks. Silahkan dibaca baik-baik tentang Langkah Mudah Perkalian Matriks ini ya.
Perkalian Skalar
Perkalian skalar didefiniskan dengan mengalikan suatu konstanta dengan setiap elemen dari suatu matriks, sehingga dihasilkan matriks baru yang memiliki ordo sama dengan matriks sebelumnya. Secara simbolis, untuk setiap bilangan real k dan matriks A, kA = [kaij]. Serupa dengan sifat aljabar pada umumnya, –A merepresentasikan perkalian skalar –1 ∙ A dan setiap pengurangan dapat dituliskan sebagai pengurangan aljabar: A – B = A + (–B). Untuk setiap matriks A, jumlah A + (–A) akan menghasilkan matriks nol Z, suatu matriks yang semua elemennya adalah nol. Matriks –A merupakan invers terhadap operasi penjumlahan dari A, sedangkan Z merupakan identitas dari operasi penjumlahan.
Contoh 1: Menghitung Operasi Matriks
Diberikan,
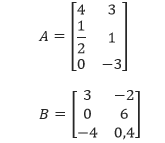
hitunglah operasi-operasi berikut ini: ½ B dan –4A – ½ B.
Pembahasan Operasi ½ B merupakan perkalian skalar terhadap matriks B. Perkalian skalar tersebut dapat dilakukan sebagai berikut.

Selanjutnya, kita akan menghitung operasi –4A – ½ B.
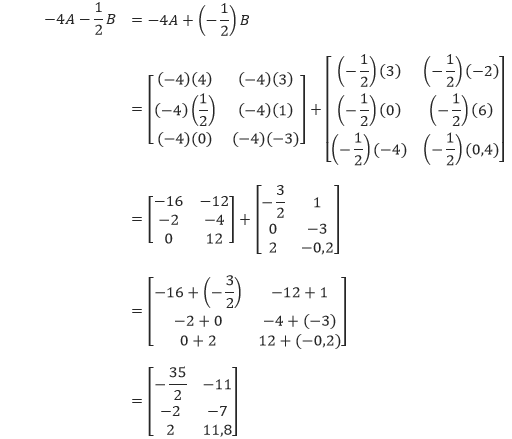
No comments:
Post a Comment