Cara Menemukan Pola Bilangan

Menemukan pola bilangan merupakan latihan yang dapat meningkatkan kemampuan dalam memberikan penalaran secara induktif (inductive reasoning). Apakah yang dimaksud dengan penalaran induktif?

Penalaran induktif (inductive reasoning) adalah suatu proses mengobservasi data, menemukan pola, dan membuat generalisasi dari hasil observasi tersebut.

Berikut ini adalah latihan yang menguji kemampuan bernalar secara induktif dalam menemukan bilangan atau huruf pada suatu barisan. Gunakanlah kemampuan bernalar secara induktif tersebut untuk melanjutkan barisan-barisan berikut!

1. 20, 18, 16, 14, –?–
2. 1, 4, 9, 16, 25, 36, –?–
3. T, Q, N, K, H, E, –?–
4. a, 6, c, 12, e, 18, –?–
5. 1, 1, 2, 3, 5, 8, 13, –?–

Pelajari pola berikut, kemudian lengkapilah persoalan tersebut berdasarkan observasimu. (Jangan menggunakan alat hitung di sini. Yang kamu cari adalah polanya, tidak hanya jawaban bilangannya)

1.	1 ∙ 1 11 ∙ 11 111 ∙ 111 1111 ∙ 1111 11111 ∙ 11111	= = = = =	1 121 12321 1234321 –?–
2.	6 ∙ 7 66 ∙ 67 666 ∙ 667 6666 ∙ 6667 66666 ∙ 66667	= = = = =	42 4422 444222 44442222 –?–
3.	123456789 ∙ 9 123456789 ∙ 18 123456789 ∙ 27 123456789 ∙ 36 123456789 ∙ –?–	= = = = =	111111111 222222222 333333333 –?– 555555555
4.	9 ∙ 0 + 1 9 ∙ 1 + 2 9 ∙ 2 + 3 9 ∙ 3 + 4 –?–	= = = = =	1 11 21 –?– 41
5.	1 + (9 ∙ 0) 2 + (9 ∙ 1) 3 + (9 ∙ 12) 4 + (9 ∙ 123) –?–	= = = = =	1 11 111 –?– 11111
6.	8 + (9 ∙ 0) 7 + (9 ∙ 9) 6 + (9 ∙ 98) 5 + (9 ∙ 987) –?–	= = = = =	8 88 –?– –?– 88888

Meningkatkan Kemampuan Bernalar (Tambahan)

Perhatikan gambar berikut.

Masing-masing huruf pada soal di atas melambangkan bilangan-bilangan yang berbeda. Pertanyaannya: berapakah nilai B dan J?

Pembahasan dari permasalahan yang terakhir, dapat dilihat di bawah ini. Jika terdapat masalah dalam melihat file pembahasan, silahkan download file pembahasan tersebut di sini.

Soal dan Pembahasan Aplikasi Deret Geometri

Barisan maupun deret geometri sering digunakan untuk menyelesaikan permasalahan yang sering kita jumpai di sekitar kita. Beberapa permasalahan yang sering menggunakan konsep barisan dan deret geometri adalah permasalahan pada ayunan bandul, depresiasi, penuaan peralatan, laju pertumbuhan populasi, dan lain sebagainya.

Soal 1: Menyelesaikan Penerapan Barisan Geometri: Bandul

Bandul adalah sembarang obyek yang digantungkan pada suatu titik tertentu dan dibiarkan untuk mengayun dengan bebas di bawah pengaruh dari gaya gravitasi. Misalkan ayunan suatu bandul masing-masing panjangnya 0,8 dari ayunan sebelumnya. Lama kelamaan, ayunan bandul tersebut akan semakin pendek dan akan berhenti (walaupun secara teoritis tidak akan pernah berhenti)

1. Seberapa panjangkah ayunan ke-6 dari bandul tersebut, apabila panjang ayunan pertamanya adalah 125 cm?
2. Berapakah panjang lintasan total yang telah dilalui oleh bandul tersebut sampai ayunan yang ke-6?
3. Butuh sampai berapa ayunankah agar panjang dari masing-masing ayunan bandul tersebut kurang dari 14 cm?
4. Berapakah panjang lintasan total yang telah dilalui bandul tersebut sampai bandul tersebut berhenti berayun?

Pembahasan Karena panjang masing-masing ayunan sama dengan 0,8 panjang ayunan sebelumnya, maka kita dapat menyimpulkan bahwa panjang ayunan bandul tersebut membentuk barisan geometri.

1. Karena panjang ayunan pertamanya adalah 125 cm, maka kita peroleh a1 = 125 dan rasionya r = 0,8. Sehingga beberapa suku pertama dari barisan tersebut adalah 125, 100, 80, dan seterusnya. Untuk suku ke-6, kita dapat menentukannya dengan menggunakan rumus:
   
   Jadi, bandul tersebut mengayun sejauh 40,96 cm pada ayunannya yang ke-6.
2. Untuk menentukan panjang lintasan total sampai ayunan ke-6, kita hitung S6.
   
   Sehingga, bandul tersebut telah menempuh 461,16 cm sampai ayunan ke-16.
3. Untuk menentukan banyaknya ayunan ketika masing-masing ayunan panjangnya kurang dari 14 cm, kita selesaikan n pada persamaan 14 = 125(0,8)n – 1.
   
   Jadi, setelah ayunan ke 10 (atau mulai ayunan ke-11), panjang dari lintasan bandul akan kurang dari 14 cm.
4. Panjang lintasan total sebelum bandul berhenti berayun sama dengan jumlah deret geometri tak hingga dengan a1 = 125 dan r = 0,8.
   
   Sehingga, panjang lintasan yang telah ditempuh oleh bandul sebelum berhenti berayun adalah 625 cm.

Soal 2: Bermain Ayunan

Rhisky sedang bermain ayunan di halaman belakang rumahnya. Dia mengayunkan ayunan tersebut dengan menggunakan tangan dan tubuhnya agar ayunan tersebut berayun sampai ketinggian maksimum, kemudian membiarkannya sampai ayunan yang dia tumpangi berhenti dengan sendirinya. Dalam setiap ayunan, Rhisky menempuh 75% dari panjang ayunan sebelumnya. Jika panjang busur pertama (atau ayunan pertama) 2 meter, tentukan panjang busur yang ditempuh Rhisky pada ayunan ke-8. Berapa meterkah total panjang busur yang ditempuh Rhisky sebelum dia berhenti berayun?

Pembahasan Diketahui panjang busur pertama yang ditempuh Rhisky adalah 2 meter, sehingga kita peroleh a1 = 2. Sedangkan dalam setiap ayunannya dia menempuh 75% dari panjang lintasan sebelumnya. Sehingga r = 75% = 0,75. Untuk menentukan panjang ayunan ke-8, kita tentukan a8 dari barisan tersebut.

Sehingga, panjang ayunan Rhisky yang ke-8 adalah 0,27 meter atau 27 cm. Selanjutnya kita tentukan panjang lintasan yang ditempuh oleh Rhisky sebelum dia berhenti berayun. Untuk menentukan panjang lintasan ini, kita cari jumlah deret tak hingga dari barisan tersebut.

Jadi panjang lintasan yang telah ditempuh oleh Rhisky sampai dia berhenti berayun adalah 8 meter.

Soal 3: Permasalahan Depresiasi

Suatu mobil SUV baru mengalami depresiasi nilai jual sebesar 15% tiap tahunnya (hal ini berarti harga jualnya menjadi 85% dari harga jual tahun sebelumnya). Jika harga beli dari mobil SUV baru tersebut adalah 510 juta rupiah, berapakah harga jual dari SUV tersebut setelah 5 tahun? Berapa tahunkah sampai harga SUV tersebut kurang dari 100 juta rupiah?

Pembahasan Harga jual suatu SUV sama dengan 85% dari harga tahun sebelumnya, sehingga kita peroleh r = 85% = 0,85. Harga beli mobil SUV baru tersebut adalah 510 juta rupiah, atau dengan kata lain a0 = 510 (dalam juta). Akibatnya, harga jual pada tahun pertama a1 = 510 ∙ 0,85 = 433,5. Sehingga dalam menentukan harga jual SUV tersebut setelah 5 tahun, kita akan tentukan a5.

Kita peroleh bahwa harga jual SUV tersebut setelah 5 tahun adalah 226,29 juta rupiah. Selanjutnya kita tentukan sampai tahun ke berapa ketika harga SUV tersebut kurang dari 100 juta rupiah. Permasalahan tersebut dapat diselesaikan dengan menentukan nilai ndari persamaan

Jadi, setelah tahun ke-10 (atau mulai tahun ke-11) harga SUV tersebut akan kurang dari 100 juta rupiah.

Cara Mengajarkan Rumus Luas Layang-Layang

Andi telah merancang layang-layang yang akan diikutkan dalam suatu perlombaan. Dia merencanakan akan menggunakan kertas berwarna hijau untuk menyampul layang-layang tersebut dan bambu sebagai diagonal-diagonalnya. Dia juga akan menghubungkan ujung-ujung diagonal tersebut dengan benang dan melipat kertas sampul sepanjang benang kemudian mengelemnya. Apabila rancangan layang-layang Andi seperti terlihat pada gambar berikut, dapatkah kamu membantu Andi untuk menentukan luas kertas layang-layang minimal untuk menyampul/menutupi layang-layang tersebut?

Untuk membantu Andi dalam menentukan luas minimal kertas yang diperlukan, kita memerlukan konsep luas salah satu bangun datar, yaitu layang-layang (kite). Mari kita temukan rumus untuk menentukan luas dari layang-layang dengan melakukan penyelidikan berikut.

Investigasi: Menemukan Rumus Luas Layang-layang

Untuk melakukan investigasi ini, kamu akan memerlukan kertas, pensil, penggaris, dan gunting. Setelah semua perlengkapan tersebut siap, lakukan langkah-langkah berikut.

1. Buatlah layang-layang pada kertas yang telah disediakan. Perhatikan bahwa layang-layang merupakan bangun datar segi empat yang memiliki tepat dua pasang sisi berurutan yang kongruen. Layang-layang memiliki sifat bahwa titik potong kedua diagonalnya membagi salah satu diagonalnya menjadi dua bagian yang sama panjang. Sehingga dalam melukis layang-layang, kita buat dahulu diagonal-diagonalnya kemudian kita hubungkan ujung-ujung diagonal tersebut dengan ruas garis.
2. Lipatlah layang-layang yang terbentuk menurut diagonal-diagonalnya. Kemudian guntinglah layang-layang menurut sisi-sisinya dan bekas lipatan yang terbentuk.
   
3. Secara coba-coba, susun kembali potongan-potongan layang-layang tersebut. Apakah dari percobaan tersebut kamu menemukan bangun datar persegi panjang?
   

Dari kegiatan di atas dapat diperoleh bahwa luas layang-layang yang memiliki panjang diagonal d1 dan d2 sama dengan luas persegi panjang yang memiliki panjang d1 dan 1/2 d2. Sehingga luas layang-layang sama dengan setengah dari perkalian panjang diagonal-diagonalnya.

Jika d1, d2, dan L secara berturut-turut adalah panjang diagonal pertama, panjang diagonal kedua, dan luas dari suatu layang-layang, maka L = 1/2 ∙ d1 ∙ d2.

Mengajarkan Perbandingan Pecahan dengan Permainan

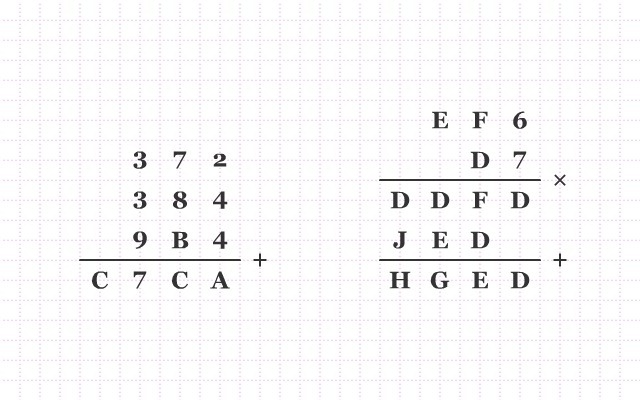
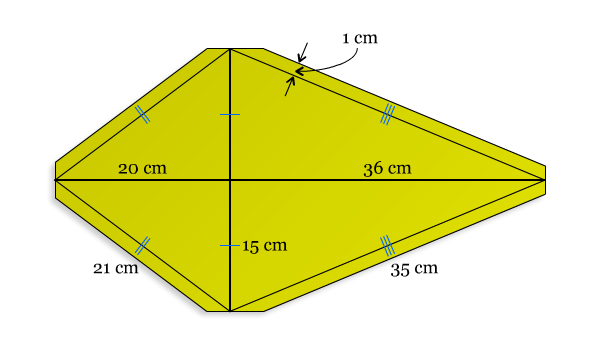
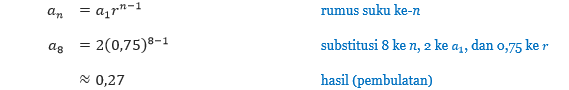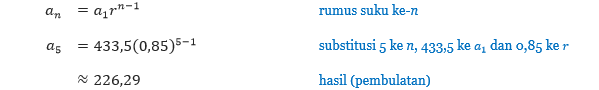Materi pecahan sering menjadi momok bagi sebagian besar siswa SD ataupun SMP. Untuk itu, mari kita pelajari pecahan dengan cara yang lebih manis, yaitu dengan game “Pesta Cokelat Maksimal”. Pada game ini kita akan belajar untuk membagi cokelat. Selain itu kita juga akan berlatih membandingkan dan mengurutkan bagian-bagian cokelat, yang digunakan sebagai konteks dari pecahan.

Aturan Game

Pada game ini membutuhkan 3 buah meja dan 6 buah cokelat. Satu, dua, dan tiga buah cokelat, yang memiliki kesamaan dalam ukuran dan rasa, secara berturut-turut diletakkan pada meja pertama, kedua, dan ketiga. Setiap tamu yang datang memilih satu dari ketiga meja tersebut kemudian duduk mengelilingi meja tersebut. Aturan dari game ini menyatakan bahwa jika semua tamu telah duduk, cokelat yang ada pada meja tersebut dibagi sama rata kepada seluruh tamu yang mengelilingi meja tersebut. Untuk tujuan dalam game ini, kita anggap bahwa semua pemain menginginkan bagian cokelat yang semaksimal mungkin, dan semua tamu yang memilih meja menganggap dirinya sebagai tamu yang terakhir.

Dan Game-pun Dilakukan

Ketika memainkan game ini, tempatkan lembar kerja di setiap meja. Lembar kerja tersebut dapat ditunjukkan oleh gambar berikut.

Semua partisipan game ini berdiri agak jauh dari meja, akan tetapi mereka juga harus jelas untuk melihat cokelat yang ada di atas meja dan semua tamu yang telah duduk mengelilingi meja tersebut. Semua partisipan juga harus memiliki copy-an dari lembar kerja di atas. Setelah setiap tamu baru yang duduk, semua partisipan (termasuk mereka yang telah duduk) harus memikirkan di mana tamu selanjutnya seharusnya duduk. Adalah hal yang penting untuk menanyakan kepada setiap tamu baru, mengapa dia memilih meja tertentu. Semua partisipan lainnya mendengarkan dengan cermat pendapat dari tamu baru tersebut untuk mendiskusikannya, apakah pendapat tamu baru tersebut benar atau salah.

Diskusi Langkah Demi Langkah Selama Game Berlangsung

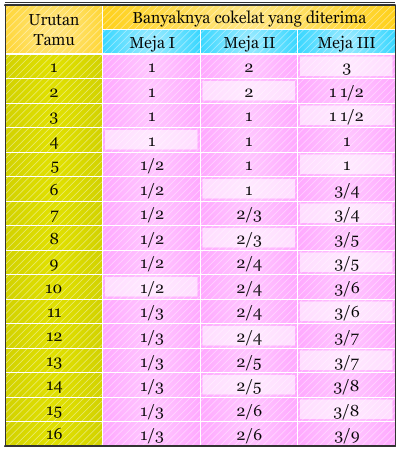
Perhatikan tabel di bawah dan ikuti penjelasannya.

Karena semua kotak cokelat pada masing-masing meja memiliki ukuran yang sama, maka kita gunakan kata “bagian” sebagai satuan dalam keseluruhan pembahasan ini. Tamu yang datang pertama kali akan memilih meja ke-3. Mengapa? Karena saat pertama kali datang, banyaknya cokelat pada meja pertama paling banyak di antara meja-meja yang lain. Tamu kedua akan mendapat 1 bagian pada meja pertama, 2 bagian pada meja ke-2, dan 1 1/2 bagian pada meja ke-3, karena 3 bagian pada meja ini akan dibagi kepada tamu sebelumnya. Sehingga tamu ke-2 akan memilih meja yang ke-2. Tamu ke-3 akan mendapat 1 bagian pada meja pertama, 1 bagian pada meja ke-2, dan 1 1/2 pada meja ke-3. Sehingga tamu ke-3 akan memilih meja ke-3.

Tamu 4, 5, dan 6

Tamu ke-4 dapat memilih sembarang meja, karena ada 1 bagian cokelat yang menunggunya pada masing-masing meja. Misalkan tamu ke-4 memilih meja yang pertama. Maka tamu ke-5 dan 6 secara berturut-turut bisa memilih meja yang ke-3 dan 2. Bagaimana jika tamu ke-4 memilih meja yang berbeda? Maka tamu ke-5 dan ke-6 memilih meja yang berbeda pula. Perhatikan gambar berikut!

Dari gambar di atas, apapun urutan meja yang dipilih oleh tamu ke-4, 5, dan 6 tidak akan mengubah bagian cokelat yang akan diterima oleh tamu ke-7, pada masing-masing meja.

Tamu Ke-7

Keputusan meja mana yang akan dipilih oleh tamu ke-7 patut mendapat perhatian yang berbeda. Tamu ke-7 akan mendapat pilihan 1/2 bagian pada meja pertama, 2/3 bagian pada meja ke-2, dan 3/4 bagian pada meja ke-3. Manakah yang paling besar: 1/2, 2/3, ataukah 3/4? Kita dapat menganggap setiap pecahan tersebut sebagai “pecahan yang kurang dari keseluruhan.” Bagaimanapun, ketiga pecahan tersebut berbeda: 1/2 sama dengan 1/2 kurangnya dari keseluruhan, 2/3 sama dengan 1/3 kurangnya dari keseluruhan, dan 3/4 sama dengan 1/4 kurangnya dari keseluruhan. Maka, kita dapat membandingkan unit-unit pecahan 1/2, 1/3, dan 1/4 terlebih dahulu. Yang dimaksud unit pecahan di sini adalah pecahan yang memiliki pembilang sama dengan 1.

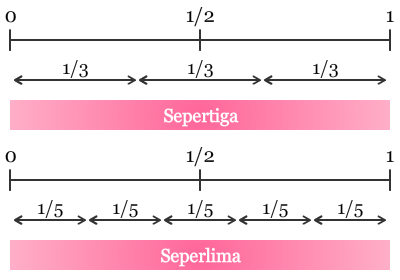
Bayangkan 3 kotak cokelat yang memiliki ukuran/besar sama. Satu kotak dibagi menjadi 2 bagian yang sama, satu kotak dibagi menjadi 3 bagian yang sama, dan satu kotak dibagi menjadi 4 bagian yang sama. Bagian manakah yang terkecil, bagian manakah yang terbesar?

Semakin banyak kita membagi cokelat, maka semakin kecil bagian cokelat yang kita dapat. Atau secara informal, kita dapat mengatakan: “Semakin banyak teman semakin bagus, akan tetapi tidak demikian apabila kita ingin membagikan cokelat.” Sehingga, 1/2 > 1/3 > 1/4. Secara matematis, kita dapat menyatakan bahwa: Beberapa unit pecahan dapat dibandingkan dengan membandingkan penyebutnya–semakin besar penyebutnya, semakin kecil nilai unit pecahan tersebut.

Bayangkan 3 kotak cokelat yang sama. Satu kotak cokelat pertama dipotong 1/2 bagian, satu kotak cokelat pertama dipotong 1/3 bagian, dan satu kotak cokelat lainnya dipotong 1/4 bagian. Dari ketiga kotak cokelat tersebut, kotak cokelat manakah yang memiliki bagian sisa yang paling besar? Jawaban dari pertanyaan ini sama dengan jawaban dari pertanyaan, “Cokelat manakah yang dipotong paling kecil?” Sehingga, 3/4 > 2/3 > 1/2. Ini berarti bahwa, tamu ke-7 harus memilih meja yang ke-3.

Tamu 8 sampai 12

Tamu ke-8 akan membandingkan 2/3 dan 3/5, karena kedua pecahan tersebut lebih besar dari 1/2. Tetapi, seberapa lebih besarkah? Untuk membandingkannya, perhatikan gambar berikut!

Dari gambar di atas, kita dapat melihat bahwa 2/3 lebih dari 1/2, sebesar setengahnya 1/3. Sedangkan 3/5 lebih dari 1/2, sebesar setengahnya 1/5. Padahal 1/5 kurang dari 1/3. Sehingga, setengahnya 1/5 kurang dari setengahnya 1/3. Hal ini menyebabkan 3/5 kurang dari 2/3. Sehingga, tamu ke-8 seharusnya memilih meja yang ke-2. Selanjutnya, tamu ke-9 pergi ke meja ke-3.

Tamu ke-10 dapat memilih meja manapun, karena dia akan mendapatkan bagian yang sama, yaitu 1/2 bagian dari kotak cokelat. Akan tetapi, pada meja ke-2 bagian yang akan diterima direpresentasikan dengan 2/4, sedangkan pada meja ke-3 direpresentasikan dengan 3/6. Sehingga, kita dapat mengatakan bahwa 1/2 = 2/4 = 3/6. Ketiga pecahan tersebut merupakan pecahan yang senilai. Apa itu pecahan senilai?

Pecahan senilai dari pecahan tertentu dapat diperoleh dengan mengalikan pecahan tertentu tersebut dengan suatu bilangan. Atau dapat disimbolkan, a/b = p/q, apabila p = k × a dan q = k × b, untuk a, b, p, q, dan k merupakan bilangan asli.

Misalkan tamu ke-10 memilih meja pertama dan tamu ke-11 memilih meja ke-3. Maka tamu ke-12 akan memilih meja ke-2.

Tamu 13

Meja manakah yang seharusnya dipilih oleh tamu ke-12? Mari kita mulai dengan membandingkan 1/3 dan 2/5. Dengan menggunakan pecahan senilai, kita dapatkan 1/3 = 2/6. Sebelumnya, kita telah mendapatkan, untuk unit-unit pecahan, semakin besar penyebutnya, semakin kecil nilai unit pecahan tersebut. Sehingga, 1/5 lebih besar dari 1/6. Sehingga pertidaksamaan itu juga berlaku bagi dua kali dari masing-masing unit pecahan tersebut. Diperoleh, 2/5 > 2/6. Sehingga aturan ini tidak hanya berlaku pada unit-unit pecahan, tetapi juga berlaku pada setiap pecahan yang memiliki pembilang sama. (Bayangkan untuk menempatkan beberapa beban yang banyaknya sama pada sisi kanan dan kiri suatu timbangan. Semua beban di sisi kiri memiliki berat yang sama, dan semua beban di sebelah kanan memiliki berat yang sama. Akan tetapi setiap beban pada sisi kiri lebih ringan daripada setiap beban di sebelah kanan. Beban manakah yang lebih ringan, semua beban di sebelah kiri atau kanan?)

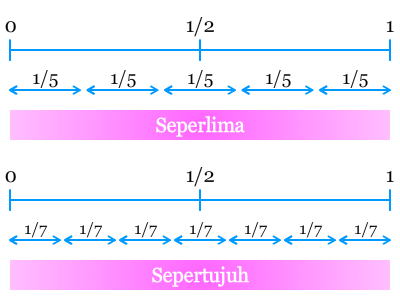
Sekarang kita akan membandingkan 2/5 dan 3/7. Untuk membandingkan kedua pecahan ini, perhatikan gambar berikut!

Dari gambar tersebut kita dapat melihat bahwa 2/5 kurang dari 1/2, yaitu sebesar setengahnya 1/5. Sedangkan 3/7 kurang dari 1/2, yaitu sebesar setengahnya 1/7. Karena 1/5 lebih besar dari 1/7, maka 2/5 terletak di sebelah kiri 1/2 lebih jauh daripada 3/7. Hal ini menunjukkan bahwa, 2/5 < 3/7, dan tamu ke-13 seharusnya pergi ke meja 3.

Dan Tamu-tamu Selanjutnya

Tamu yang ke-14 mungkin mengatakan bahwa telah ditunjukkan 1/3 = 2/6 < 2/5. Dengan menggunakan penalaran ini, 1/3 = 3/9 < 3/8. Sehingga kita perlu membandingkan 2/5 dan 3/8. Sebelumnya kita telah mendapatkan bahwa 2/5 kurang dari 1/2, yaitu sebesar setengahnya 1/5. Atau dengan kata lain, 2/5 kurang dari 1/2 sebesar 1/10. Atau,

Di sisi lain, 1/2 = 4/8 dan 3/8 sama dengan 1/8 kurangnya dari 1/2, atau

Lagi, seperti kasusnya tamu ke-7, kita mengurangkan pecahan yang sama, tetapi 1/10 lebih kecil dari 1/8. Sehingga, 2/5 lebih besar dari 3/8, dan meja ke-2 harus dipilih oleh tamu ke-14. Selanjutnya, tamu ke-15 harus memilih meja ke-3. Tamu ke-16 mendapatkankan bagian yang sama di setiap meja.

Setelah tamu ke-16 tersebut, kita dapat menghentikan permainan ini. Walaupun secara teoritis, permainan ini dapat diteruskan sampai tamu yang tak terbatas

Kesebangunan Pada Segitiga Siku Siku

Kesebangunan dapat digunakan untuk menyelesaikan permasalahan yang ada di sekitar kita. Sebagai contoh, kesebangunan dapat digunakan untuk menghitung tinggi suatu benda yang sulit diukur secara langsung. Suatu pohon yang tinggi menjulang memiliki panjang bayangan 37,5 m di suatu pagi dan 12,5 m di suatu sore. Apabila sinar-sinar garis dari puncak pohon yang menuju tanah membentuk sudut siku-siku, dapatkah kamu menghitung tinggi pohon tersebut?

Sebelum menghitung tinggi pohon tersebut, kita pelajari terlebih dahulu mengenai kesebangunan pada segitiga siku-siku. Perhatikan gambar berikut.

Dari gambar tersebut, apakah kamu menduga bahwa segitiga PSR sebangun dengan segitiga RSQ? Dapatkah kamu membuktikannya? Segitiga PSR memang sebangun dengan segitiga RSQ. Berikut pembuktiannya.

Perhatikan bahwa sudut PSR dan sudut RSQ merupakan sudut siku-siku, sehingga besar sudut PSR sama dengan sudut RSQ, yaitu 90°. Selanjutnya, pada segitiga PRQ, besar sudut RPS sama dengan 180° dikurangi jumlah dari besar sudut SQR dan 90°. Demikian juga pada segitiga RSQ, besar sudut QRS sama dengan 180° dikurangi jumlah dari sudutSQR dan 90°.

Sehingga, besar sudut PRQ sama dengan besar sudut QRS. Karena pada segitiga PSR dan segitiga RSQ terdapat dua sudut yang sama besar, maka kedua segitiga tersebut sebangun. Karena segitiga PSR dan segitiga RSQ merupakan segitiga-segitiga yang sebangun, maka perbandingan dari panjang sisi-sisi yang bersesuaian besarnya sama.

Selanjutnya, coba buktikan bahwa segitiga PSR sebangun dengan segitiga PRQ dan segitiga RSQ sebangun dengan segitiga PRQ. Dari kesebangunan segitiga-segitiga tersebut, diperoleh beberapa persamaan berikut.

Sehingga, dari segitiga PQR dan ruas garis RS dengan titik S terletak pada sisi PQsedemikian sehingga ruas garis RS tegak lurus dengan sisi PQ, diperoleh ketiga persamaan berikut.

RS = √(SP ∙ SQ); RP = √(PS ∙ PQ); dan RQ = √(QS ∙ QP)

Dari persamaan tersebut, kita dapat menghitung tinggi pohon pada permasalahan awal. Tinggi pohon tersebut adalah √(37,5 ∙ 12,5) = 21,65 m

Cara Menentukan Akar Kuadrat Bilangan

Yudis diminta oleh gurunya untuk membuat poster tentang lingkungan. Poster tersebut haruslah berbentuk persegi dengan luas maksimum 46.656 mm2. Akan tetapi Yudis bingung untuk membuat poster tersebut, karena dia kurang mengerti persegi yang luasnya 46.656 mm2 tersebut memiliki panjang sisi berapa. Dapatkah kamu membantu permasalahan Yudis tersebut?

Seperti kita ketahui, luas persegi sama dengan kuadrat dari panjang sisinya. Apabila luas persegi diketahui, dapatkah kalian menentukan panjang sisinya? Panjang sisi persegi dapat ditentukan dengan menggunakan operasi kebalikan dari kuadrat, yaitu akar kuadrat.

Untuk menentukan panjang sisi dari persegi yang luasnya 46.656 mm2, kamu harus menentukan akar kuadrat dari 46.656, yaitu √(46.656). Bagaimana cara menentukan akar kuadrat dari 46.656? Berikut ini akan dibahas mengenai bagaimana cara menentukan akar kuadrat dari 46.656 dengan cara bersusun dan faktorisasi prima.

Menentukan Akar Kuadrat dengan Cara Bersusun

Untuk menentukan akar kuadrat dengan cara bersusun, perhatikan ilustrasi berikut!

1. Kelompokkan bilangan 46.656 dua angka dari belakang dengan menggunakan garis ataupun titik, sehingga akan terbentuk 4 | 66 | 56. Cari taksiran rendah untuk √4, yaitu kelompok angka paling depan. Taksiran rendah dari √4 = 2. Tulis 2 × 2 di sebelah kiri dan tulis juga hasilnya di bawah 4.
2. Kurangkan 4 dengan 4, tulis hasilnya di bawah. Turunkan dua angka selanjutnya. Jumlahkan angka sebelah kiri, yaitu 2 + 2 = 4. Selanjuntya carilah angka yang sama sehingga hasil 4_ × _ merupakan bilangan bulat terbesar yang kurang dari atau sama dengan 66. Diperoleh bilangan tersebut adalah 1, sehingga 41 × 1 = 41. Kurangkan 66 dengan 41, tulis hasilnya, yaitu 25, di bawah.
3. Turunkan 2 angka selanjutnya. Jumlahkan angka sebelah kiri kedua, yaitu 41 + 1 = 42. Tulis hasilnya di bawah. Carilah angka yang sama sehingga 42_ × _ merupakan bilangan bulat terbesar yang kurang dari atau sama dengan 2.556. Diperoleh bilangan tersebut adalah 6, sehingga 426 × 6 = 2.556. Kurangkan 2.556 dengan 2.556, kemudian tulis hasilnya di bawah. Akar dari 46.656 merupakan bilangan yang terdiri dari angka-angka yang berwarna orange. Sehingga, √46.656 = 216.

Setelah mengetahui cara menentukan akar kuadrat dengan cara bersusun, sekarang perhatikan cara lainnya berikut.

Menentukan Akar Kuadrat dengan Faktorisasi Prima

Untuk menentukan akar kuadrat dari 46.656, ubahlah bilangan tersebut ke dalam bentuk perkalian faktor-faktor primanya. Untuk membantu, kamu dapat menggunakan pohon faktor atau cara sengkedan.

Sehingga diperoleh, 46.656 = 26 × 36 = (23 × 33)2 = 2162. Oleh karena itu, √46.656 = 216

Sifat Sifat Trapesium

Trapesium merupakan bangun datar segi empat yang tepat memiliki sepasang sisi yang sejajar. Pada trapesium, sisi-sisi yang sejajar disebut sebagai alas trapesium. Sedangkan pasangan sudut yang memiliki kaki sudut pada sisi alas yang sama disebut pasangan sudut alas. Selanjutnya, kita akan menyelidiki sifat-sifat dari trapesium.

Investigasi: Apa sajakah Sifat-sifat Trapesium?

Langkah 1: Gunakanlah dua sisi dari penggaris untuk melukis ruas garis sejajar dengan panjang yang tidak sama antara satu dengan yang lain. Lukis dua ruas garis tidak sejajar yang menghubungkan ruas garis yang telah terbentuk untuk membuat trapesium.

Langkah 2: Gunakanlah busur derajat untuk menemukan jumlah dari besar sudut-sudut alas berdekatan di antara sisi alas. Apa yang dapat kamu peroleh dari jumlah sudutnya?

Apa yang kamu selidiki pada langkah 2 merupakan salah satu dari sifat trapesium. Sifat trapesium tersebut dapat dituliskan sebagai berikut.

Sifat Jumlah Sudut yang BerdekatanJumlah sudut-sudut yang berdekatan di antara sisi-sisi alas jumlahnya 180°.

Selanjutnya, kita akan menyelidiki sifat-sifat dari trapesium sama kaki. Trapesium sama kaki adalah trapesium yang sisi-sisi tidak sejajarnya sama panjang.

Langkah 3: Gunakanlah dua sisi pada penggaris untuk melukis dua garis sejajar. Gunakan jangka untuk membuat dua garis kongruen, tetapi tidak sejajar, yang menghubungkan dua ruas garis sejajar yang baru terbentuk untuk membuat trapesium sama kaki.

Langkah 4: Ukurlah masing-masing pasangan sudut-sudut alas. Apa yang dapat kamu peroleh dari besar pasangan sudut-sudut alas?

Berikut ini sifat pasangan sudut-sudut alas dari trapesium sama kaki.

Sifat Trapesium Sama KakiPasangan sudut-sudut alas dari trapesium sama kaki besarnya sama.

Selain pasangan sudut-sudut alasnya, apakah ada lagi bagian dari trapesium sama kaki yang kongruen?

Langkah 5: Lukis kedua diagonal trapesium sama kaki. Bandingkanlah panjang dari masing-masing diagonal tersebut dengan menggunakan jangka. Apa yang dapat kamu simpulkan?

Sifat Diagonal-diagonal Trapesium Sama KakiDiagonal-diagonal dari trapesium sama kaki kongruen

Contoh Soal dan Pembahasan Faktorisasi Polinomial

Dalam melakukan faktorisasi suku banyak (polynomial), terdapat 3 langkah yang biasanya ditempuh:

1. Perhatikan apakah masing-masing suku memiliki Faktor Persekutuan Terbesar(FPB) yang tidak satu.
2. Perhatikan apakah polynomial tersebut dapat difaktorkan dengan carapengelompokan.
3. Perhatikan apakah polynomial tersebut masuk ke dalam kasus khusus.

Faktor Persekutuan dan Faktor Persekutuan Terbesar

Faktor Persekutuan (Common Factor, Common Divisor) adalah bentuk aljabar (bisa berupa konstanta, variabel, atau perkalian keduanya) yang dapat membagi suku-suku polynomial. Faktor Persekutuan Terbesar (Greatest Common Factor, Greatest Common Divisor) adalah faktor persekutuan yang bernilai paling besar dan dapat membagi suku-suku polynomial. Cara yang paling mudah dalam mencari FPB adalah dengan memfaktorkan masing-masing suku terlebih dulu. Setelah itu, FPB dikeluarkan ke luar tanda kurung.

Contoh 1:

• 5x + 10 = 5 ∙ x + 5 ∙ 2 = 5(x + 2)
• 12x2 – 9x = 2 ∙ 2 ∙ 3 ∙ x ∙ x – 3 ∙ 3 ∙ x = 3x(4x – 3)

Pemfaktoran dengan Cara Pengelompokan

Sebelum melakukan pemfaktoran dengan pengelompokan, harap untuk selalu memperhatikan apakah suku-suku dalam polynomial memiliki FPB yang tidak satu atau tidak.

Contoh 2:
6abx + 9ax – 2bx – 3x
= x(6ab + 9a – 2b – 3)
= x([6ab + 9a]  + [–2b – 3])
= x(3a[2b + 3] – [2b + 3])
= x(3a – 1)(2b + 3)

Dalam pemfaktoran dengan cara pengelompokan, biasanya digunakan untuk memfaktorkan polynomial yang bersuku 4. Pertama, dari keempat suku polynomialbagilah ke dalam dua kelompok. Masing-masing kelompok berilah tanda kurung. Yang perlu diperhatikan adalah bahwa minimal satu grup dalam pengelompokan tersebut memiliki faktor persekutuan. Setelah itu, keluarkan faktor persekutuan keluar tanda kurung pada masing-masing kelompok. Bentuk aljabar yang ada di dalam kurung haruslah sama. Apabila tidak sama, maka ada kesalahan dalam membagi kelompok atau memang polynomial tersebut tidak dapat difaktorkan dengan cara pengelompokan. Jadi diperlukan sedikit kecermatan dalam membagi kelompok suku-suku polynomial.

Contoh 3A:
5xy + 2y – 20x – 8
= (5xy – 8) + (2y – 20x)
= (5xy – 8) + 2(y – 10x)
Kesalahan dalam pembagian kelompok.

Contoh 3B:
5xy + 2y – 20x – 8
= (5xy + 2y) + (–20x – 8)
= y(5x + 2) – 4(5x + 2)
= (y – 4)(5x + 2)

Contoh 4:
x + 2xy + 3y + 5
= (x + 2xy) + (3y + 5)
= x(1 + 2y) + (3y + 5)
Bentuk aljabar dalam kurung tidak sama, dan dengan pengelompokan lain juga akan menghasilkan bentuk aljabar dalam kurung yang tidak sama, soal tersebut tidak dapat difaktorkan dengan cara pengelompokan.

Pemfaktoran dengan cara pengelompokan juga dapat digunakan dalam memfaktorkan polynomial bentuk ax2 + bx + c, dengan a, b, dan c adalah bilangan real. Jika tidak terdapat suatu bilangan di depan salah satu suku x, maka bilangannya adalah 1.

Contoh 5:
2x2 + x – 5
a = 2; b = 1; c = –5

Cara memfaktorkan trinomial, polinomial dengan 3 suku, adalah dengan mengubahnya dari 3 suku menjadi 4 suku. Langkah pertama adalah mencari 2 bilangan yang dijumlahkan menghasilkan b, dan jika dikalikan menghasilkan ac. Jika tidak dapat ditemukan kedua bilangan yang memenuhi, maka trinomial tersebut tidak dapat diselesaikan dengan cara pengelompokan. Setelah ditemukan 2 bilangan yang memenuhi,pecahlah b menjadi penjumlahan dari kedua bilangan tersebut. Setelah itu, permasalahannya dapat diselesaikan seperti contoh 2 – 4.

Contoh 6:
x2 + 2x – 15. Cari dua bilangan yang dijumlahkan hasilnya 2, jika dikalikan hasilnya 1 ∙ 15 = 15. Dengan sedikit perhitungan, kedua bilangan tersebut adalah 5 dan –3. Setelah itu pecahlah b = 2 menjadi penjumlahan dari kedua bilangan tersebut. Sehingga 2x = 5x – 3x. Diperoleh,

x2 + 2x – 15
= x2 + 5x – 3x – 15
= x(x + 5) – 3(x + 5)
= (x – 3)(x + 5)

Contoh 7:
6x2 – 5x – 4
= 6x2 – 8x + 3x – 4
= 2x(3x – 4) + (3x – 4)
= (2x + 1)(3x – 4)

Pemfaktoran Kasus Khusus

Berikut ini adalah kasus khusus dalam pemfaktoran yang perlu diingat.

a2 – b2 = (a + b)(a – b) a3 + b3 = (a + b)(a2 – ab + b2) a3 – b3 = (a – b)(a2 + ab + b2)

Contoh 8:
x2 – 9 = (x + 3)(x – 3)

Contoh 9:
x3 + 8 = x3 + 23 = (x + 2)(x2 – 2x + 4)

Contoh 10:
8x3 – 27 = (2x)3 – 33 = (2x – 3)(4x2 + 6x + 9)

Substitusi

Cara substitusi digunakan untuk pemfaktoran trinomial bentuk ax2m + bxm + c, dengan a,b, c, dan m bilangan real. Yang perlu dilakukan adalah dengan memisalkan u = x2, kemudian difaktorkan secara biasa. Setelah difaktorkan dalam u, substitusi u dengan x2.

Contoh 11:
x4 – 4x2 – 45; misal u = x2
= u2 – 4u2 – 45
= (u – 9)(u + 5)
= (x2 – 9)(x2 + 5)
= (x + 3)(x – 3)(x2 + 5)

Contoh 12:
(x – 2)2 – 9; misal u = x – 2
= u2 – 9
= (u + 3)(u – 3)
= (x – 2 + 3)(x – 2 – 3)
= (x + 1)(x – 5)