Selamat datang, Kali ini kita akan berbagi tentang Rumus Sinus. Silahkan dibaca baik-baik tentang Rumus Sinus ini ya.
Permasalahan trigonometri biasanya melibatkan segitiga siku-siku. Akan tetapi pada segitiga yang bukan siku-siku, tidak tertutup kemungkinan dapat diselesaikan dengan menggunakan trigonometri. Misalkan jika diketahui besar dua sudut dalam segitiga dan panjang satu sisinya, kita dapat menentukan panjang kedua sisi lainnya dengan menggunakan aturan sinus (law of sines). Aturan sinus berhubungan dengan luas dari segitiga. Mari kita cari tahu bagaimana trigonometri dapat membantu kita untuk menemukan luas dari segitiga PQR berikut.
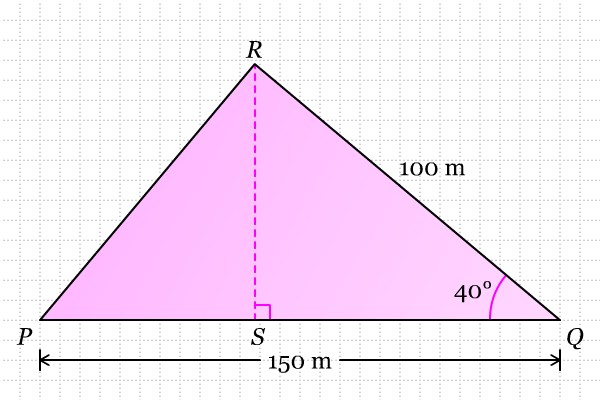
Perhatikan bahwa PQ merupakan alas segitiga, dan RS merupakan tinggi segitiga. Untuk menentukan panjang segmen RS, kita dapat menggunakan segitiga siku-siku QRS. Sisi QRmerupakan hypotenusa dari segitiga QRS karena terletak di depan sudut siku-siku S.
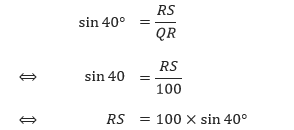
Selanjutnya kita tentukan luas dari segitiga PQR yaitu setengah kali alas kali tinggi.
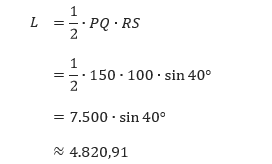
Jadi, luas segitiga PQR adalah 4.820,91 m2.
Selanjutnya kita akan menyelidiki rumus umum untuk menentukan luas segitiga apabila diketahui panjang dua sisinya dan besar sudut yang diapitnya.
Investigasi 1: Menemukan Rumus Luas Segitiga
- Carilah luas dari masing-masing segitiga berikut. Gunakan contoh di atas sebagai panduan.

- Dari langkah nomor 1, temukan rumus untuk menentukan luas segitiga dalam bentuka, b, dan θ.
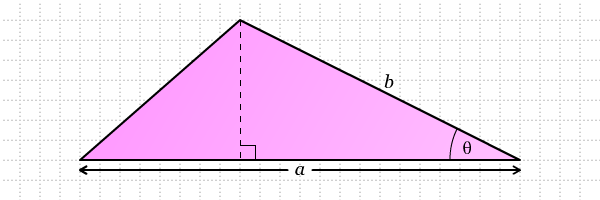
Apa yang dapat kita simpulkan dari penyelidikan di atas? Dari penyelidikan di atas, kita telah menemukan rumus untuk menentukan luas segitiga jika diketahui panjang kedua sisinya dan besar satu sudut yang diapitnya.
Rumus luas segitiga adalah L = 1/2 ∙ a ∙ b ∙ sin θ, dengan a dan b adalah panjang sisi-sisi segitiga, sedangkan θ adalah besar sudut yang diapit kedua sisi tersebut.
Sekarang, kita gunakan rumus luas segitiga yang baru kita peroleh untuk menurunkan sifat trigonometri pada sembarang segitiga, yang disebut aturan sinus.
Investigasi 2: Aturan Sinus
Perhatikan segitiga ABC berikut.
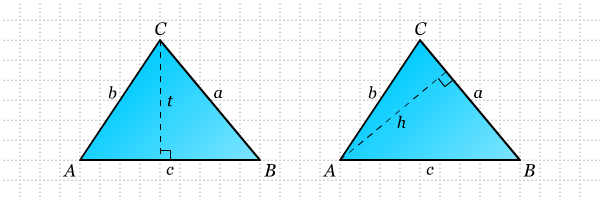
- Tentukan t dalam bentuk a dan sin dari suatu sudut tertentu.
- Tentukan t dalam bentuk b dan sin dari suatu sudut tertentu.
- Gunakan aljabar untuk menunjukkan: (sin A) / a = (sin B) / b.
- Sekarang perhatikan segitiga ABC yang sama tetapi dengan menggunakan tinggi yang berbeda, yaitu h. Tentukan h dalam bentuk c dan sin dari suatu sudut tertentu.
- Tentukan h dalam bentuk b dan sin dari suatu sudut tertentu.
- Gunakan aljabar untuk menunjukkan (sin B) / b = (sin C) / c.
Dari penyelidikan ke-2 di atas kita menemukan 2 rumus, yaitu pada langkah 3 dan langkah 6. Dengan mengkombinasikan kedua rumus tersebut, diperoleh rumus berikut:
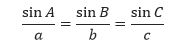
Hasil penyelidikan ke-2 di atas dapat dirangkum menjadi seperti berikut:
Untuk suatu segitiga yang memiliki sudut-sudut dalam A, B, dan C serta sisi-sisi yang panjangnya a, b, dan c (a di depan A, b di depan B, c di depan C), maka: (sin A) / a = (sin B) / b = (sin C) / c.
Dari aturan sinus yang baru saja diperoleh, kita dapat menentukan panjang sisi segitiga jika diketahui panjang satu sisi yang lain dari segitiga tersebut dan besar dua sudut dalamnya. Selain itu, kita juga dapat menentukan besar sudut dalam segitiga dengan menggunakan aturan sinus, apabila kita tahu apakah sudut yang kita cari tersebut lancip ataukah tumpul.
No comments:
Post a Comment